Plato's Quadruple

Number Theory Level 3

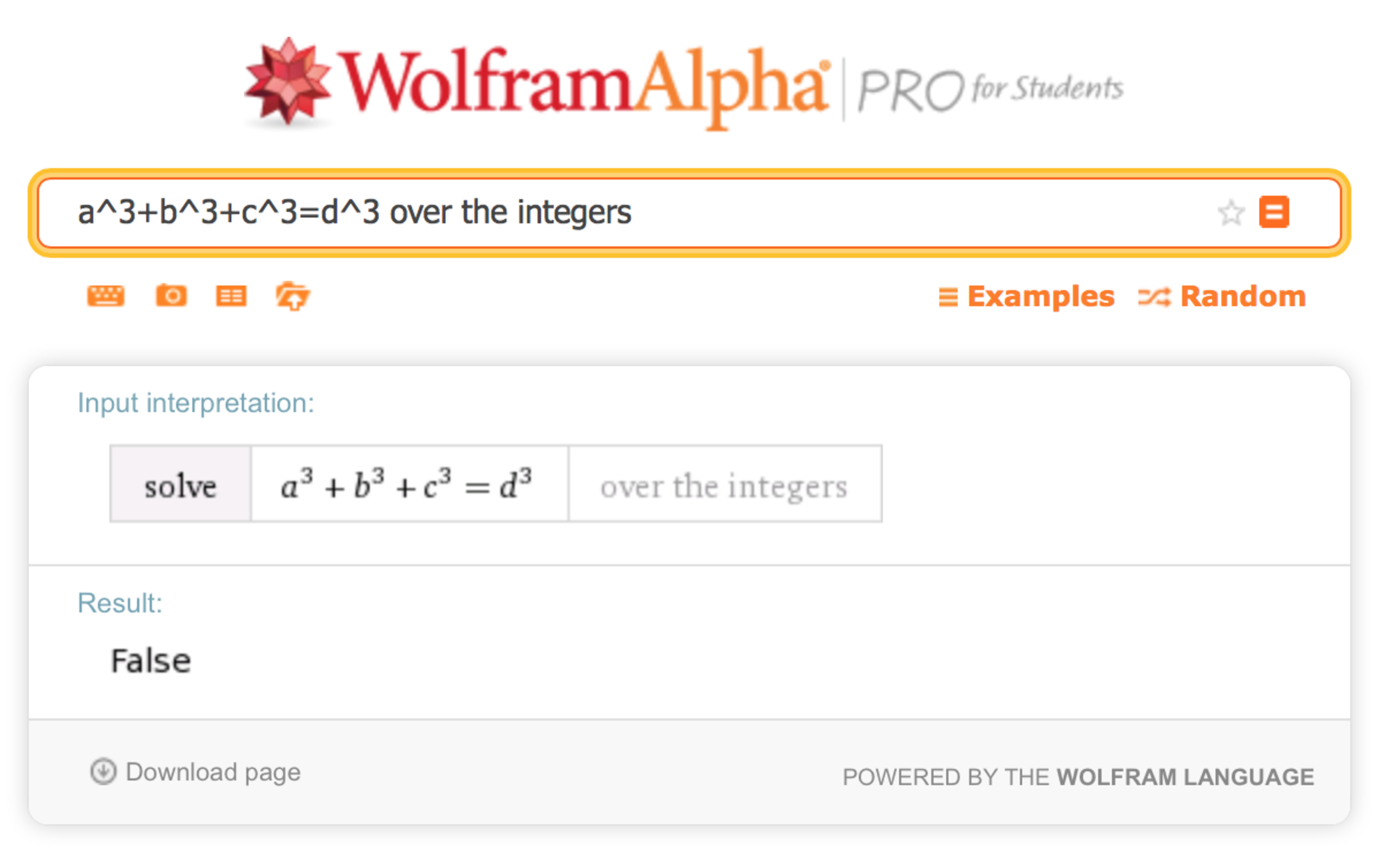
According to Wolfram|Alpha, the equation $a^3+b^3+c^3=d^3$ has no solutions in the integers. However, this is not the case!

There are, in fact, infinite solutions to this equation, and the minimal solution is quite extraordinary. Where $a$ , $b$ , $c$ and $d$ are positive integers, our minimal solution takes the following form:

$a^2+b^2=c^2$ $a^3+b^3+c^3=d^3$

If $(a,b,c,d)$ is our minimal solution, what is $a+b+c+d$ ?

The answer is 18.

2 solutions

Garrett Clarke
Jul 18, 2015

Simply checking the first pythagorean triple $(3,4,5)$ gives us our solution:

$3^2+4^2=5^2$ $3^3+4^3+5^3=27+64+125=216=6^3$

Therefore our minimal solution is $(3,4,5,6)$ , and our answer is $3+4+5+6=\boxed{18}$ .

Any non hit and trial method??

Naman Kapoor - 5 years, 11 months ago

I wish I had one! The problem is related to Fermat's Last Theorem, and as you may know, that problem didn't go unsolved for hundreds of years for no reason!

Garrett Clarke - 5 years, 11 months ago

Actually, there are several parameterizations of this equation here

Daniel Liu - 5 years, 11 months ago

Maggie Miller
Jul 18, 2015

As a side note, I believe Wolfram Alpha gives "False" because it interprets letters from the beginning of the alphabet as constants (so of course as constants it's not always true that $a^3+b^3+c^3=d^3$ ). It gives a different answer if you use letters from the end of the alphabet, which it interprets as variables. (Still not very useful, though.)

Haha yes, thank you Wolfam|Alpha :P

Garrett Clarke - 5 years, 11 months ago

Plato's Quadruple

The answer is 18.

2 solutions

0 pending reports