Play-Doh-Nut
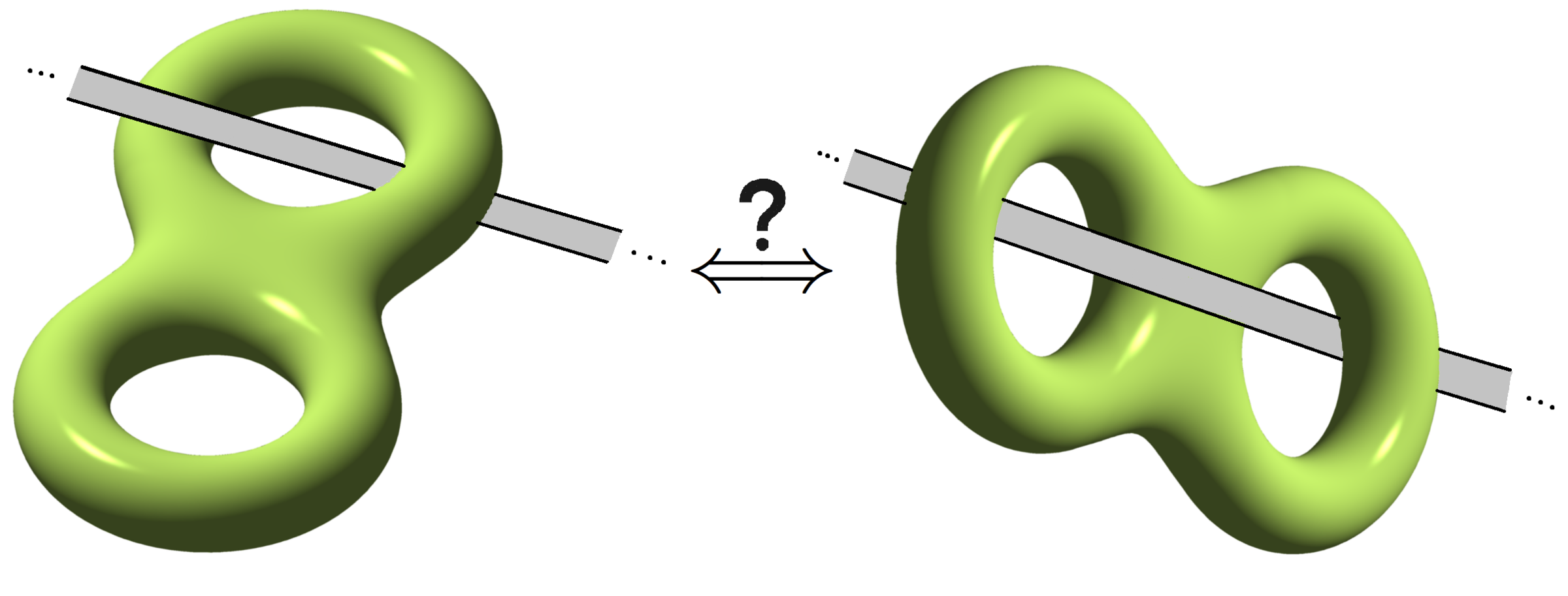
Above is an imagine of a two holed torus with an infinitely long pole through it.
On the left side we have the pole going through one hole and on the right we have the pole going through two holes.
Is it possible to deform the torus with the pole going through one hole so it becomes the torus with the pole going through both holes?
Details: The pole is rigid and cannot be moved. It is also impossible to slide the torus off the edge of it, it's infinitely long.
The torus is made of a Play-Doh like material. It can stretch but it cannot be ripped, you cannot stick two pieces of it together, you cannot pass it through itself and holes cannot be created or destroyed.
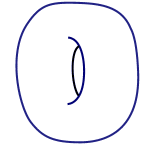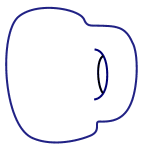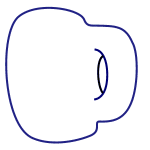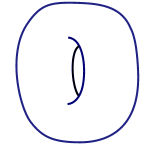
To show you what is allowed, here is an example of a donut (one holed torus) deforming into a coffee cup.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I will explain each step, it might be hard to see what voodoo is happening.
1 . We shirnk one of the holes and enlarge the other hole.
2 . We slide the smaller hole along the pole untill it is inline with the bigger hole.
3 . We shrink the big hole and notice the pole no longer goes through it...
Thus it is shown that they can be deformed into eachother.
In my question I asked "Is it possible to deform the torus with the pole going through one hole so it becomes the torus with the pole going through both holes?" but I showed in my picture that the torus with a pole through two holes can be deformed into a torus with a pole through one hole. This is alright since each step in my picture is reversible which makes the two statements equivalent.
What happens if we consider an n holed torus?