Playing Children
 At 6pm, 15 boys left school, and then the remaining children could be split evenly into groups each containing 2 girls and 1 boy.
At 6pm, 15 boys left school, and then the remaining children could be split evenly into groups each containing 2 girls and 1 boy.
At 7pm, 45 girls left school, and then the remaining children could be split evenly into groups each containing 1 girl and 5 boys.
How many boys were there before 6pm?
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Typo: At 7pm there are 5 boys for every GIRL.
Love your reasoning, thank you!
if we consider total of 25 groups '23 groups was broken by parents who take away 45 girls as each group contain 2 girls. so the number of girls left become 5. now look at no of boys in the group which is 25 so 2nd made group is perfectly become at the ratio of 1:5. now add no of boys that leave early (15) with no of boys in the end (25). 15+25=40
g/(b-15) = 2/1, (g-45)/(b-15)=1/5.... solving g=50, b= 40
ugh why didnt i think of that!
x=girls, y=boys. after taking 15 boys the ratio of girls to boys x:y = 2:1, after taking 45 girls the new ratio is x-45:y = 1:5, solving for y = 25 plus the first 15 boys taken = 40.
let initial there are x boys and y girls, after 6 pm there will be (x-15) boys and y girls so dividing 2 girls and 1 boys groups then we can say that [y=2(x-15)] and after 7 pm there will be (x-15) boys and (y-45) girls so dividing 1 girls and 5 boys then we can say that (x-15)=5(y-45) . solve both equations find x? which will be 40 after solving the equations.
Let N be the number of groups that could be split evenly at 6 pm, with each containing 2 girls and 1 boy; thus the number of girls and number of boys before 6 pm can be represented as 2N and N+15 respectively while at 6 pm, 2N girls and N boys were still at school. At 7 pm, it is stated that 45 girls left school and that the remaining children could be split evenly into groups each containing one girl and five boys.
So to get the value of N, we first can conclude that the number of groups that could be split evenly at 7 pm is equivalent to N/5, since at 7 pm there were N boys left and each group contains 5 boys, thus dividing N by 5 to get the number of groups that can be formed at 7 pm. This value is equal to (2N–45)/1, which is just equal to (2N–45). Cross multiplying, you get 10N–225=N. Here you'll get N=25. Since N is also the equivalent value of the number of boys at 6 pm when 15 boys left school, then the number of boys before 6 pm would be just N+15, which is equal to 25+15=40. Since the question asks how many boys were there before 6 pm, the answer is 40 boys.
I hope this solution will be helpful to many, thanks. :)
I am willing to accept critical comments and if anyone doesn't understand this solution, please feel free to ask. :))
Moderator note:
Good clear explanation!
the ratio of boys and girls when 15 boys left 2/1=girls/(boys-15) --eq(1) and ratio when 45 girls left 1/5=(girls-45)/(boys-15) ----eq(2) solve equation 1 and 2 boys = 40
Before 6 pm, there are 'b' boys and 'g' girls in total.
At 6, 15 boys leave: Changing the student count to 'b-15' boys and 'g' girls.
The children can be grouped, such that there are 2 girls for every 1 boy in the class. Mathematically this means
g = 2 × ( b − 1 5 ) = 2 b − 3 0
2 b − g = 3 0
At 7, 45 girls leave: Student count now is 'b-15' boys and 'g-45' girls.
The children are grouped again, such that there are 5 boys for every 1 girl in the class.
b − 1 5 = 5 × ( g − 4 5 )
5 g − b = 2 1 0
Substituting g = 2 b − 3 0 gives:
1 0 b − 1 5 0 − b = 2 1 0
9 b = 3 6 0 ⟹ b = 4 0
at 6pm, boys:girls=5:10; at 7pm, boys:girls= 5:1; it is means that 45girls are left 9 from 5 group. so after 6pm there are 25 boys. 25+15=40.
let there be 2x girls and x boys 2x:x=2:1. When 45 girls left it became 2x-45:x=1:5.Therefore 5(2x-45)=x. x=25. Therefore 1*25 boys were there=25. 15 boys were taken away. Therefore no. of boys in total=15+25=40.
let x no. of groups be formed first then A.T.Q 2x+x+15 is the total no. of student let in second case y no. of groups be formed han A.T.Q y+5y+15+45 is the total no. of student comparing both we get x+15=5y+15 i.e. x=5y and 2x-y=45 hence solving no. of boys=40
Its simple... just consider 50 girls and 40 boys. 15 boys leave. 25 boys left. And then 45 girls left so just 5 remain.Now we have 25 boys and 5 ggirls. So for every 5 boys there is 1 girl left
Easiest to work things backwards.
Let's say x groups can be formed in the end, so there'd be x girls & 5x boys. Before the girls left, there must be x+45 girls & 5x boys, with girl : boy ratio equals to 2 : 1.
x + 45 = 2(5x) = 10x
9x = 45
x = 5
Answer
= 5x + 0 + 15
= 40
Let the number of groups at 6pm be x
Let the number of groups at 7pm by y
Since the number of boys remains constant after 6pm,
x=5y
And since there is a difference of 45 girls later,
2x=y+45
Using substitution,
10y=y+45
9y=45
y=5
So number of boys = 5(5)+15 =40
Transform the ratios into time slots. 6pm the ratio is 10:5 (G:B) and 7pm it is 1:5 (G:B). The only change that has occurred is -45 girls, which reduced the ratio by 9x. Therefore, each girl is equal to 5 boys. Plugging that in to the 6pm slot we get 25 boys, then adding the 15 that left at that time we get 40.
Boys = x (at first)
Girls = y (at first)
6pm
x - 15
Ratio
Boys : Girls
x - 15 : y
2 : 1
7pm
y - 45
Ratio
Boys : Girls
x - 15 : y - 45
5 : 1
Assumptions and Facts
. Boys stayed the same throughout 6 - 7pm
. In the first ratio it was 2 : 1 (Girls : Boys)
. In the second ratio it was 1 : 5 (Girls : Boys)
. Lets make the boy ratio the same
First ratio:
10 : 5
Second ratio:
1 : 5
. Girls decreased by 1 0 9
1 0 9 = 45
1 0 1 0 = 50
Girls = 50
Boys = 40
Moderator note:
Good way of creating the compound ratio which allows us to compare these numbers easily.
g:(b-15)=2:1 ....equation 1
(g-45):(b-15)=1:5....equation 2 Criss cross method from 1st equation g=2b-30 Put that in 2nd equation b = 40
2(x-15)=y equation1 and 5(y-45)=x-15 equation2. Solve these two equations to get the answer.
Boys= 40 Girls= 50
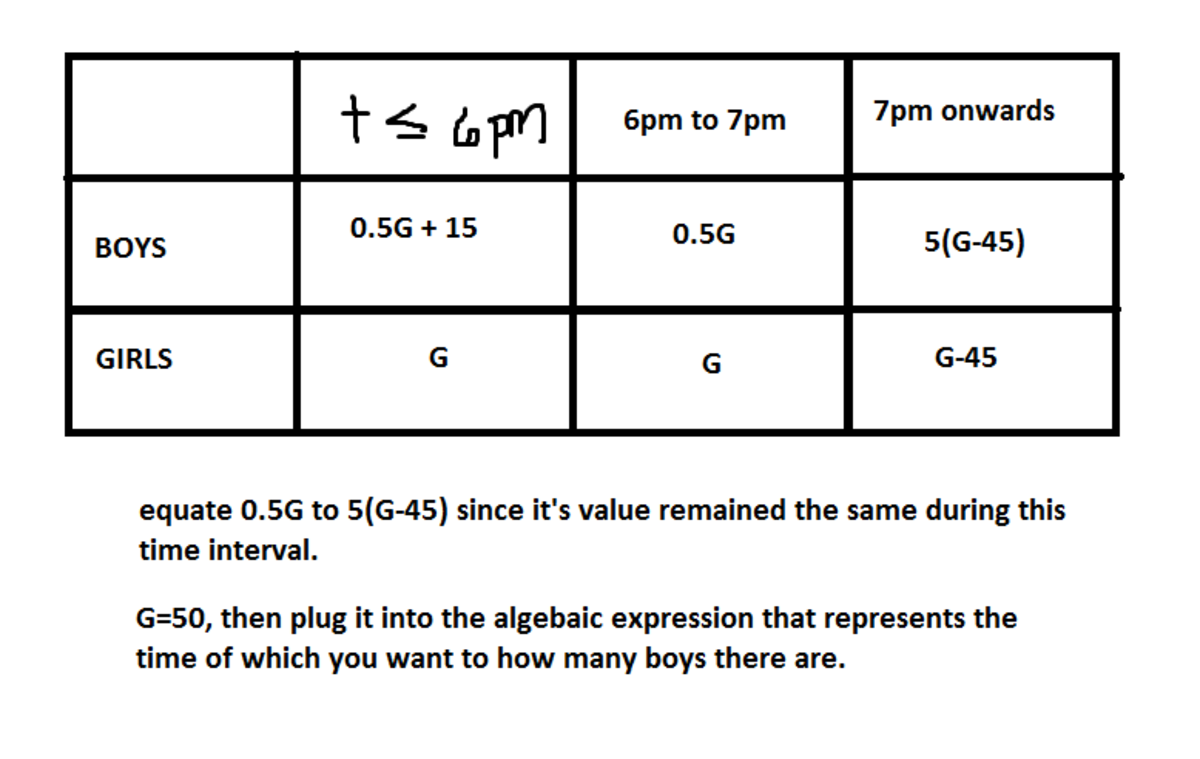
At 6 PM, there are 2 girls for every boy, so 2 b = g .
At 7 PM, there are now g − 4 5 girls and there are 5 boys for every boy, so 5 ( g − 4 5 ) = b .
Thus, 5 ( g − 4 5 ) = 2 g , so g = 5 0 .
The number of boys at 6 PM was 2 5 0 = 2 5 , so the number of boys before 6 PM was 2 5 + 1 5 = 4 0 .