Playing in an Ampere-ian World!
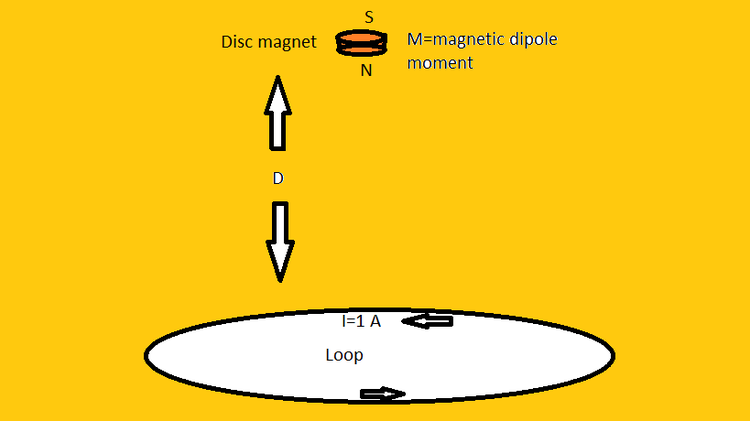 There is a circular current carrying loop of radius
, it has a current
passing through it, and its North (anti-clockwise face) is facing upward
There is a circular current carrying loop of radius
, it has a current
passing through it, and its North (anti-clockwise face) is facing upward
Suppose, i place a thin disc magnet of mass with negligible dimensions over it that has a Magnetic moment of , such that the north pole is facing downwards at height above the loop.
Derive an expression for the force of interaction In Newtons between them, and submit the value for the given details.
Details and assumptions
- 1 g
- Am
- 10 cm
- cm
- A
- Take the magnetic permeability for vacuum to be
Note, to derive the expression, you may use the model of magnetic charges, also neglect negligible terms, I assure you that all information you need has been given.
The answer is 0.0001348.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
You can solve this problem in 3 way i will introduce each of them.
For axial-symmetry field you can easy derive that the force acting on a dipole moment p m is F = − p m d z d B Putting B = 2 μ 0 i ( R 2 + z 2 ) 2 3 R 2
We will find that F ( z = d ) = 2 3 p m μ 0 i ( R 2 + d 2 ) 2 5 R 2 d
If you interpret dipole as 2 monopole of magnetic charge q m and distance a then p m = q m a . Using the fact that force is equal to F ( z ) = q m B ( z ) and again you will get
F ( z = d ) = 2 3 p m μ 0 i ( R 2 + d 2 ) 2 5 R 2 d
3.Third Newton's law
You can first find the force of magnetic moment using the formula for field of magnetic moment and then by third Newton's law the force is same and again you get
F ( z = d ) = 2 3 p m μ 0 i ( R 2 + d 2 ) 2 5 R 2 d
Note: You can apply third Newton's law on magnetic force only if two magnetic moments as a vector are parallel!
So the correct answer is
F ( z = d ) = 2 3 p m μ 0 i ( R 2 + d 2 ) 2 5 R 2 d = 1 . 3 4 8 ˙ 1 0 − 4 N