Playing with a set square

Geometry Level pending

This is a problem that I designed two years ago while I was playing with a set square. 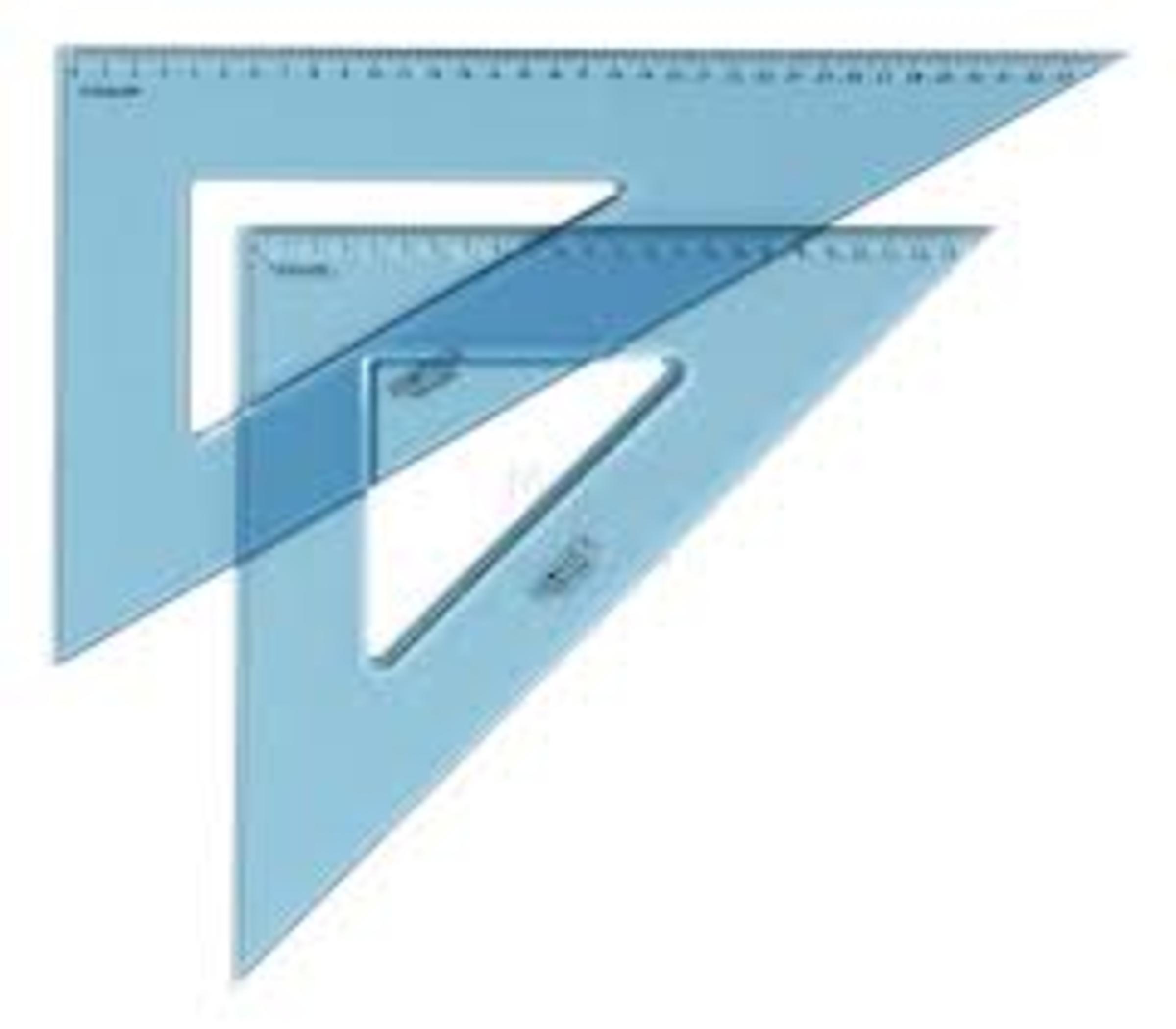Well, as shown below, there are two right-angled triangles ABE and ADC that share the point A where is located the right angle.

Knowing that A B ‾ \overline{AB} = 36 A D ‾ \overline{AD} = 28 Find the area of the triangle EFC

Round your answer to 3 decimal places

Clarification: E B ‾ \overline{EB} meet C D ‾ \overline{CD} at F

A,E and C belong to the same line.

A,D and B belong to the same line.

∠ \angle ABE= ∠ \angle AEB= 4 5 ∘ 45^{\circ}

∠ \angle ADC= 6 0 ∘ 60^{\circ}

(The picture above is a scale drawing)


The answer is 106.677.

Andrea Virgillito by Andrea Virgillito , 22, Italy

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Andrea Virgillito
Feb 16, 2017

Let H be the projection of F on A B ‾ \overline{AB} . FHB is isosceles thus: F H ‾ \overline{FH} = H B ‾ \overline{HB}

H D ‾ \overline{HD} = F H ‾ \overline{FH} x tan ⁡ \tan 30 ∘ ^{\circ} = F H ‾ 3 \frac{\overline{FH}}{\sqrt{3}}

H B ‾ \overline{HB} - H D ‾ \overline{HD} = D B ‾ \overline{DB} = 8 (36-28=8)

So H B ‾ \overline{HB} - H B ‾ 3 \frac{\overline{HB}}{\sqrt{3}} = 8 solving for H B ‾ \overline{HB} we get that it is equal to 8 3 3 − 1 \frac{8\sqrt{3}}{\sqrt{3}-1} .

The height of the triangle EFC = A H ‾ \overline{AH} = A B ‾ \overline{AB} - H B ‾ \overline{HB} = 36 - 8 3 3 − 1 \frac{8\sqrt{3}}{\sqrt{3}-1} = 28 3 − 36 3 − 1 \frac{28\sqrt{3}-36}{\sqrt{3}-1}

While the base is A C ‾ \overline{AC} - A E ‾ \overline{AE} = 28 3 − 36 28\sqrt{3}-36

The Area of the triangle EFC = 1 2 \frac{1}{2} ( 28 3 − 36 28\sqrt{3}-36 )* 28 3 − 36 3 − 1 \frac{28\sqrt{3}-36}{\sqrt{3}-1} = 106.677 \boxed{106.677}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...