Playing With an Elliptic
The equation of the elliptic curve shown here is
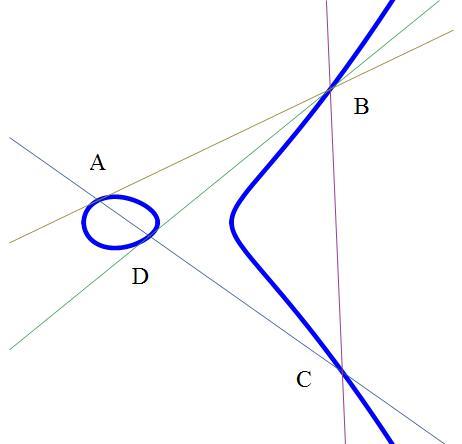
The thick blue line of the curve and the lines through points are all drawn accurately to scale. All four points have rational coordinates, but only one of them has an integer coordinate (either or ). The area of the triangle is rational and can be expressed as , where and are coprime integers.
Find the first 3 digits of the numerator
Lines through and are tangents to the elliptic curve, and both meet at point which is on the elliptic curve. Line through and intersect the elliptic curve at .
Use of calculator or computer is recommended for computations.
Corrected courtesy of Jon Haussmann
The answer is 233.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
An important property of elliptic curves, which are of the form
y 2 = x 3 + a x + b
is that for rational a , b , a line passing through 2 rational points on the curve will pass through a 3rd rational point. For this reason, elliptic curves are one of the most studied curves in algebra and number theory, which has led to the Taniyama-Shimura conjecture which in turn has led to Wiles' proof of Fermat's Last Theorem.
It's not hard to find the first point with an integer coordinate, which is
A = ( − 4 , 2 3 )
A point that is a tangent is the same as a line passing "through 2 rational points", so next point can be found in this manner
B = ( 1 4 4 1 6 8 1 , 6 9 1 2 6 2 2 7 9 )
From this, point D can be determined, which works out to a neat
D = ( − 9 5 , − 2 7 2 5 )
From points A and D , we find the last one
C = ( 9 6 1 1 2 0 0 5 , − 2 9 7 9 1 3 0 1 3 5 0 )
Using the general formula for finding areas of polygons defined by vertex coordinates, i.e.
2 1 ( ( x 1 y 2 − y 1 x 2 ) + ( x 2 y 3 − y 2 x 3 ) + ( x 3 y 1 − y 1 x 2 ) )
we finally end up with the area
1 5 2 5 2 9 9 2 2 3 3 3 0 7 6 6 9 9
and so the answer is 2 3 3
This correct answer was pointed out by Jon Haussmann.
Note: A line passing through a rational point on an elliptic that is tangent to it somewhere else cannot be assumed to be passing through another rational point, as not all solutions to quadratic equations are rational.