Playing with Pencils
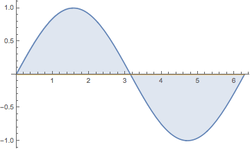 Betsy is drawing with a mechanical pencil. She ends up drawing the closed figure shown above. All units are in
inches
.
Betsy is drawing with a mechanical pencil. She ends up drawing the closed figure shown above. All units are in
inches
.
This figure is given by the formula sin(x) from 0 to 2 . Betsy desides to shade in the parts that are shaded in on the graph. She then decides to trace the outer ends of the figure with a thickness of 1/50 of an inch without lifting her pencil.
She uses 1 piece of graphite after drawing 80.56 . Let a be the number of these figures (with the shaded and outlined areas) that she can draw with this 1 piece of graphite. Find a +1.
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
What we are asked to find in this question is how many of these figures I can draw with one piece of graphite. To do this, I first need to find the total area of the figure. To do this, I will break the problem down.
a. Because we know the equation for the graph and the bounds, we can plug in this data to the formula for finding the area under a curve,
AREA = ∫ a b f ( x ) d x
and our formula becomes:
AREA = ∫ 0 2 π sin ( x ) d x
because -cos(x) is the antiderivative of sin(x), we just take − cos ( 2 π ) − ( − c o s ( 0 ) ) which ends up being 0. Uh-oh, this isn’t too good, we didn’t end up getting any area. This doesn’t make sense. But what does this tell us? This tells us that we have a net area of 0, which can help us deduce that:
∫ 0 π sin ( x ) d x = ∫ π 2 π sin ( x ) d x
So we just need to find ∫ 0 π sin ( x ) d x and double it. So we end up with − cos ( π ) − ( − c o s ( 0 ) ) = 2 and double it to obtain 4 inches 2 , the area under the shaded region.
A. We must first find the area of the curved region.
Arc Length = ∫ a b 1 + ( f ′ ( x ) ) 2 d x
Which when we plug in our known variables and simplify turns out to be: ∫ 0 2 π 1 + cos 2 x d x
Which approximates to 7.6404 .
B. We mustn’t forget about the straight orange line from 0 to 2 π .
C. We add 2 π to 7.6404 and multiply by our line width which is 1/50 of an inch. This approximates to 13.923585307 * .02 = .278471706 inches 2
We need to add the area of the shaded region to the outlined area and we obtain 4.278471706 inches 2 .
Now comes the easy part. We set up a proportion. If 1 piece of graphite can draw 80.56 inches 2 then how many times can our figure with area 4.278471706 inches 2 be drawn with this piece of graphite?
8 0 . 5 6 1 = 4 . 2 7 8 4 7 1 7 0 6 x 1
which simplifies to 8 0 . 5 6 = 4 . 2 7 8 4 7 1 7 0 6 x and then x = 1 8 . 8 2 9 1 5 3 3 8 4
So we can draw 18.829153384 figures per piece of graphite. We are asking how many figures we can draw, and because drawing 18.8 figures is not the same as drawing 19 figures, we must take the floor of 18.829153384 which is 18. We then add one to 18 and get 1 9 .