Playing with Right-Angled Triangles!

Geometry Level 4

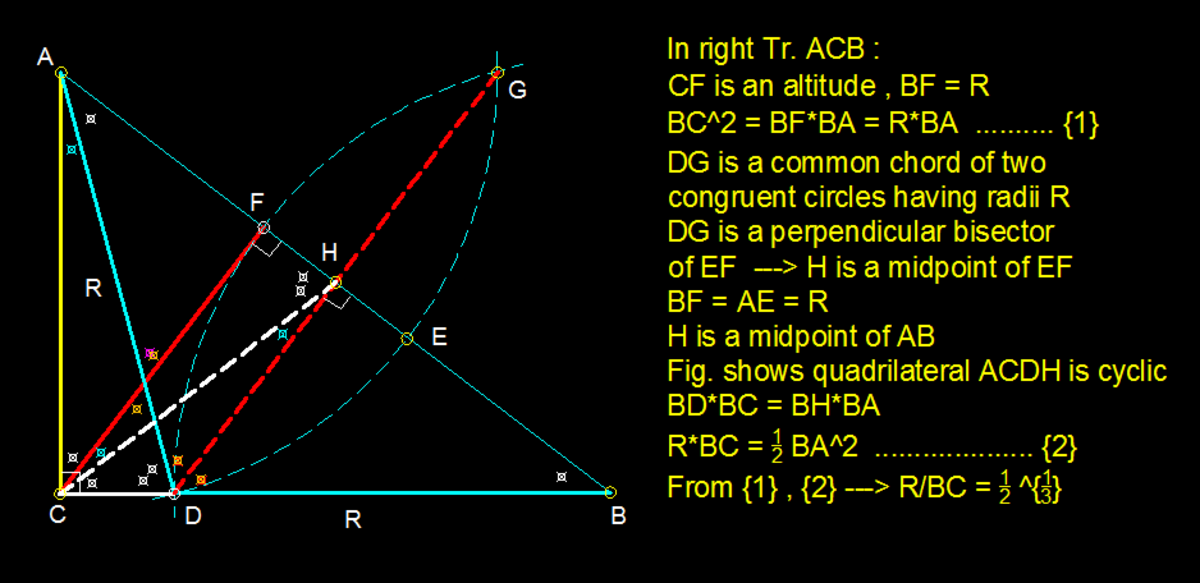
Let A B C ABC be a right-angled triangle with hypotenuse A B AB and altitude C F CF , where F F lies on A B AB . The circle through F F centred at B B and another circle of the same radius centred at A A intersect on the side C B CB . If the ratio between the lengths of F B FB and B C BC can be expressed as ( A B ) C / D \left( \dfrac{A}{B} \right)^{C/D} , for positive integers A , B , C , D A,B,C,D , find the minimum value of A + B + C + D A+B+C+D .


The answer is 7.

Satyajit Mohanty by Satyajit Mohanty , 24, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Michael Mendrin
Sep 22, 2015

Let A B C ABC be the right angled triangle, where C F CF is perpendicular to A B AB and such that the following are true

A X = X B = F B = 1 AX=XB=FB=1

C B = x CB=x

Then using geometry, ratios and Pythagoreans, we have the following

C X = F Y = x − 1 CX=FY=x-1

A C = 2 x − x 2 AC=\sqrt { 2x-{ x }^{ 2 } }

Y B = x 2 YB=\sqrt { \dfrac { x }{ 2 } }

F Y = x 2 ( x − 1 ) FY=\sqrt { \dfrac { x }{ 2 } } \left( x-1 \right)

So we just have this to solve

F Y + Y B = 1 = x 2 ( x − 1 ) + x 2 = x 3 2 FY+YB=1=\sqrt { \dfrac { x }{ 2 } } (x-1)+\sqrt { \dfrac { x }{ 2 } } =\sqrt { \dfrac { { x }^{ 3 } }{ 2 } }

with the solution x = 2 1 3 x={ 2 }^{ \frac { 1 }{ 3 } }

Hence, the ratio between FB and BC is the inverse of the cube root of 2 2

This is a particularly interesting problem because if one cheats, one can by means of compass and ruler derive the cube root of 2 2 , which is normally an impossibility and a classic problem in geometry.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

This is a particularly interesting problem because if one cheats, one can by means of compass and ruler derive the cube root of 2 2 , which is normally an impossibility and a classic problem in geometry.

Correct! I had also noticed this fact while solving the problem. Although I didn't cheat.

Satyajit Mohanty - 5 years, 8 months ago

Log in to reply

Cheating at construction problem is a time-honored tradition, such as nuesis and origami methods, which does greatly extend the range of solvable construction problems, including this one.

Michael Mendrin - 5 years, 8 months ago

The solution may be simplified by exploring similar triangles.

From the construction of the circles, it follows that XY is the perpendicular bisector of AB. We have three similar triangles: △ Y B X ≅ △ F B C ≅ △ C B A . \triangle YBX \cong \triangle FBC \cong \triangle CBA. If h = AB, a = BC, and r is the radius of the circles, this implies B C B A = B Y B X = B F B C ∴ a h = h / 2 r = r a . \frac{BC}{BA} = \frac{BY}{BX} = \frac{BF}{BC} \ \ \therefore \ \ \frac{a}{h} = \frac{h/2}{r}=\frac{r}{a}. Multiply the first two ratios and equate it to the square of the third ratio: a h ⋅ h / 2 r = ( r a ) 2 ∴ ( r a ) 3 = 1 2 . \frac{a}{h}\cdot\frac{h/2}{r} = \left(\frac{r}{a}\right)^2\ \ \therefore\ \ \left(\frac{r}{a}\right)^3 = \frac12. The desired ratio is x = r a = ( 1 2 ) 1 / 3 , x=\frac{r}{a}=\left(\frac12\right)^{1/3}, so the solution is 7.

Arjen Vreugdenhil - 5 years, 8 months ago

Log in to reply

A even neater proof, no need for pesky Pythagoreans!

Michael Mendrin - 5 years, 8 months ago
Ahmad Saad
Dec 16, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...