Please help Ed!

I have a different approach to this problem.

A figure drawn could help us, but don't worry, we can picture the scene in mind.

Let's draw a line from Ed's eye perpendicular to the wall. It will divide the bigger right angle triangle in two smaller right angle triangle. Say, the lower triangle has an angle $\theta$ with the wall. So, the upper has $90^0-\theta$ .

Clearly, $\tan\theta=\frac{30}{6}=5$ . So, $\tan(90^0-\theta)=\cot\theta=\frac{1}{5}$ .

With these simple ratios, we can say, the portion of wall in the upper triangle is $5$ times larger than the distance from Ed's eye to the wall. It's 150 , then.

Now now, the answer is 156 .

Getting the hypotenuse of the lower triangle h = sqrt of (30^2 +6^2)

sin T = 30ft / h1 T = 78.69 degrees cos T = h1 / h2 h2 = 156

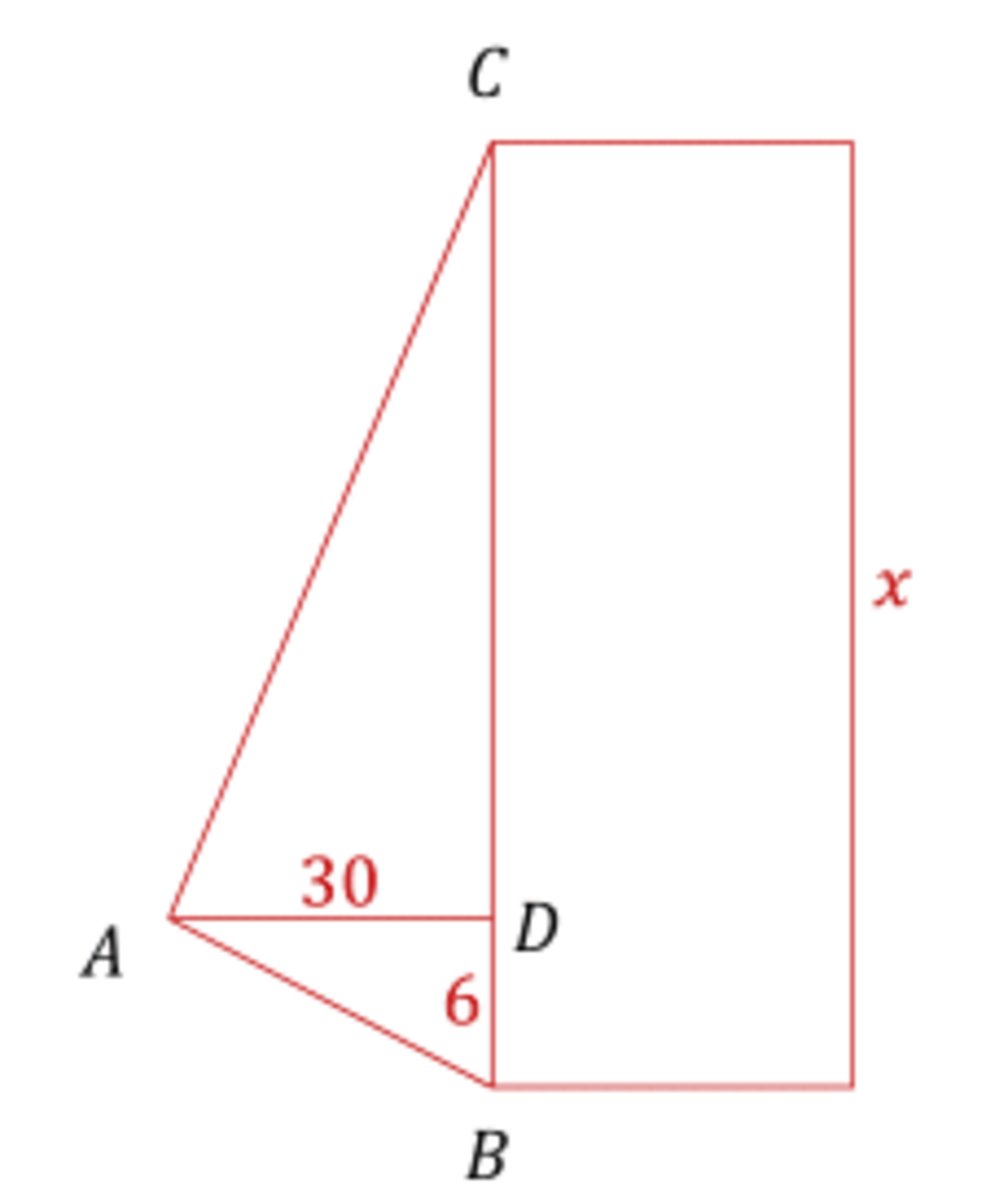Triangles $ADB$ and $CDA$ are similar, so $\frac{30}{6}=\frac{x-6}{30}$ . Solve for $x$ to get $x=156.$

let \(\h) be the height of the building

\(\cos\theta\ = \frac{height of his eye}{distance from his eye to the foot of the building} = \frac{6}{\sqrt{6^2 +30^2}} = \frac{\sqrt{6^2 +30^2}}{h}\)

$\frac{6}{\sqrt{6^2 +30^2}} = \frac{\sqrt{6^2 +30^2}}{h}$

solving for \(\h)

\(h = \boxed{156}\)

Can someone help ? Latex formatting doesn't work !!!

Let's consider 2 right triangles. One (called "Big") that Ed uses for measuring and one (called "Small") created between Ed, the ground and the building wall.

Let's consider "h" the Hypotenuse of the "Small" so that \­( { h }^{ 2 }={ 6 }^{ 2 }+{ 30 }^{ 2 }=936 \­)

Let's consider "H" the Hypotenuse of the Big

The two triangles have complementary angles.

Let's consider \­(\alpha \­) the angle of the corner of the small triangle where Ed is in positioned. \­(\alpha \­) is also the angle of the corner of the big triangle in contact with the bottom of the building.

Then \­( \cos ( \alpha )=\frac { 6 }{ h } =\frac { h }{ H } \­) Then \­( H=\frac { { h }^{ 2 } }{ 6 } =\frac { 936 }{ 6 } = \boxed{156} \­)