Plus An Obstruction (Corrected)
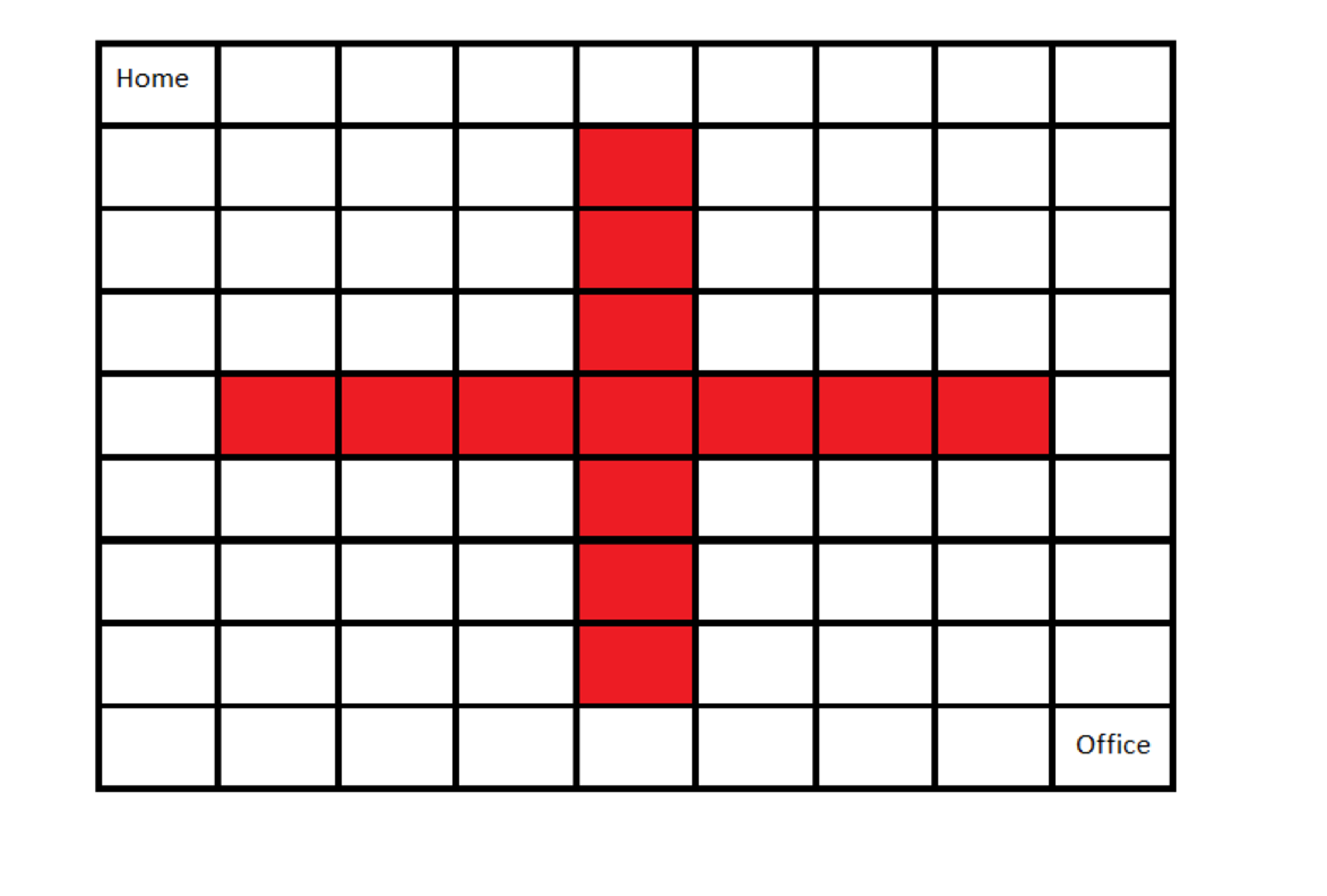 Harry lives in a
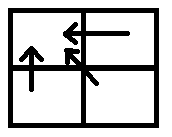
grid, where his home is in top left corner and office in bottom right corner. He wants to go to his office to work, and then come back home without visiting a cell twice. While going to office, he is only allowed to move one cell right, one cell down, or one cell diagonally below to the right:
Harry lives in a
grid, where his home is in top left corner and office in bottom right corner. He wants to go to his office to work, and then come back home without visiting a cell twice. While going to office, he is only allowed to move one cell right, one cell down, or one cell diagonally below to the right:
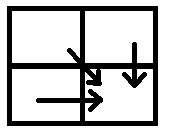
While going home, he is only allowed to move one cell left, one cell up , or one cell diagonally above, towards left:
Also, Harry can't pass through the cells marked red on the topmost grid. In how many ways can Harry go to office and come back home ?
The answer is 31752.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
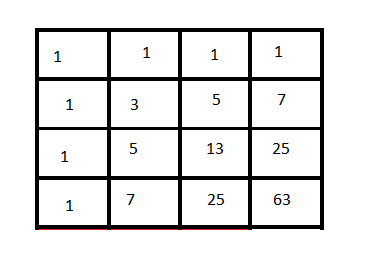
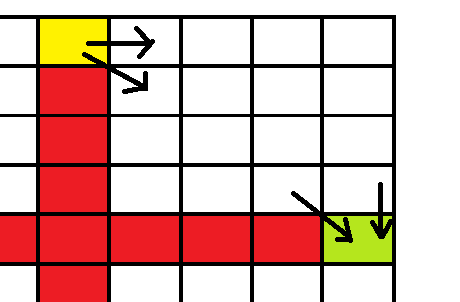
There are 1 2 6 ways to get from the top center to the right center.
By symmetry, there are also 1 2 6 ways to get from the left center to bottom center.
Giving a total of 1 2 6 × 2 = 2 5 2 ways to get to work.
Since only the main path not chosen to get to work is available for the return home, there are only 1 2 6 ways to get home.
Grand total: 2 5 2 × 1 2 6 = 3 1 7 5 2