Plus/Minus Challenge

Since $\displaystyle\sum_{k=1}^{7} k = 28$ we need to find a subset of $\{2,3,4,5,6,7\}$ whose elements sum to $\dfrac{28}{2} = 14$ in order to fulfill the given challenge. As there are in fact $4$ such subsets, namely

$\{3,4,7\}, \{2,5,7\}, \{3,5,6\}, \{2,3,4,5\},$

the given challenge can indeed be satisfied. For example, with $\{3,4,7\}$ we have that

$1 + 2 - 3 - 4 + 5 + 6 - 7 = 0.$

In general, $\displaystyle\sum_{k=1}^{n} \dfrac{n(n + 1)}{2}$ will need to be even in order for there to be a subset of $\{2,3,4, ...., n\}$ whose elements sum to $\dfrac{n(n + 1)}{4}.$ This will be the case when $n(n + 1) \equiv 0 \pmod{4},$ i.e., when either $n$ or $n + 1$ is a multiple of $4.$

When $n$ is a (positive) multiple of $4,$ then the required subset can be created as follows. Since the set $\{1,2,3, .... ,n\}$ contains $\dfrac{n}{2}$ pairs which sum to $n + 1,$ from the set $\{2,3, ...., n\}$ we will be able to choose $\dfrac{n}{4}$ pairs that sum to this value, in which case the sum of the elements of this subset will be the desired $\dfrac{n(n + 1)}{4}.$

When $n + 1$ is a positive multiple of $4,$ then the required subset can be created as follows. In the set $\{2,3, ..... ,(n - 1)\}$ there will be $\dfrac{n - 3}{2}$ pairs which sum to $n + 1.$ We can then choose $\dfrac{n - 3}{4}$ of these pairs along with the element that has the value $\dfrac{3(n + 1)}{4},$ (which will be "available" if we choose the previous pairs judiciously), to achieve a sum of

$(n + 1)*\dfrac{n - 3}{4} + \dfrac{3(n + 1)}{4} = \dfrac{(n^{2} - 2n - 3) + (3n + 3)}{4} = \dfrac{n^{2} + n}{4} = \dfrac{n(n + 1)}{4}.$

For example, with $n = 11,$ we can choose $\dfrac{11 - 3}{4} = 2$ of the $4$ pairs which sum to $12,$ say $(4,8)$ and $(5,7),$ along with $\dfrac{3(11 + 1)}{4} = 9$ to obtain a subset whose elements sum to $2*12 + 9 = 33 = \dfrac{11(11 + 1)}{4}$ as required.

Thus we can conclude that the general challenge can be satisfied if and only if either $n$ or $n + 1$ is a positive multiple of $4.$

The answer is Yes !

$\large 1-2+3+4-5+6-7=0$

Here's how I've found the solution, consider the equation $1 + 2 + 3 + 4 + 5 + 6 + 7 =28$ . If we were to replace any of the plus sign with minus sign, then, we will be subtracting twice a integer.

Trial and error:

$1 + 2 + 3 + 4 + 5 + 6 - 7 = (1 + 2 + 3 + 4 + 5 + 6 + 7) - 2(7) = 28 - 14 = 14$
$1 + 2 + 3 + 4 - 5 + 6 - 7 = (1 + 2 + 3 + 4 + 5 + 6 + 7) - 2(5 + 7) = 28 - 24 = 4$
$1 - 2 + 3 + 4 - 5 - 6 - 7 = (1 + 2 + 3 + 4 + 5 + 6 + 7) - 2(2+5 + 7) = 28 - 28 = 0$

Hence, there exist a solution, and it is $1 - 2 + 3 + 4 - 5 - 6 - 7 = 0$ .

Using a very, very simplified form of this question, we can take the sum of all the numbers, which is all the natural numbers below and equal to seven. This gives us 28. Now logic dictates that if the total is 28, that we need to find a way to get positive fourteen and negative fourteen. So we can find an example of this with 1-2-3-4-5+6+7=0. Because we have both sides that add up to positive fourteen (+1,+6+7) and the other side of negative fourteen(-2,-3,-4,-5) this will add to zero. This can be done with any two sets adding to positive fourteen and another to negative fourteen (for this question). However, using such simple terms will not be able to generalize the inclusion of a variable. For the sake this is meant to be a simple solution, I will exclude the bonus from this solution.

This is just one set of examples. I shall attend to the general case tomorrow.

$\large{\pm 1\pm2-\mp3-\mp 4\pm5\pm6-\mp7}$

One can easily notice that $0=1+2-3$ . Thus the task actually becomes $\Large \ \square \ 4 \ \square \ 5 \ \square \ 6 \ \square \ 7 = 0$ This is equal to $0$ once the sum of any 2 numbers is equal to the sum of the other remaining 2 numbers.This is clearly fulfilled by the pairs of numbers ${4,7}$ and ${5,6}$ . Thus, we just need to ensure that the signs on any pair is identical and opposite to the signs on the other pair.

Hence, $\large{1+2-3+4-5-6+7}$ or $\large{-1-2+3-4+5+6-7}$

A more intuitive proof:

Every group of 4 consecutive numbers ABCD can be made to add to zero with the operations A-B-C+D (and also -A+B+C-D) Therefore, every group of 4n consecutive numbers can also be made to add to zero by grouping them in fours. To find a solution for a group of 4n-1 numbers that starts with 1, simply add 0 at the start to get a group of 4n. (You can always make the number 1 have a plus by flipping all the pluses and minuses)

So the solution for 7 becomes: -0+1+2-3 -4+5+6-7 or 1+2-3-4+5+6-7

Finally, note that adding or subtracting an odd number always changes the oddness of the sum, so you need an even number of odd numbers in the group to be able to get to 0 (an even sum). That means that only 4n and 4n-1 are possible.

You can group the numbers in pairs that add up to $7$ :
$7; 1, 6; 2, 5; 3, 4$

(Ok, fine, one of them is a single number. That's allowed, too)

If the number of these pairs is even, there exists a solution. For half the pairs, each number gets a positive sign while the other half gets a negative sign. The question is phrased in such a way that $1$ has to have a positive sign, so we also know $6$ must have a positive sign.

Using this method, we have these possible solutions:
$1-2+3+4-5+6-7=0$
$1+2-3-4+5+6-7=0$
$1-2-3-4-5+6+7=0$

Since every pair adds up to seven and we assign both members of each pair the same sign, we are essentially adding or subtracting $7$ with each pair. Give half the pairs the opposite sign and you end up at $0$ .

This can be generalised, too: As long as we have an even number of pairs and all the pairs add up to the same number, this same technique can be used.

There are two solutions: 1) 1+2-3+4-5-6+7 = 0

2) 1+2-3-4+5+6-7 = 0

1+2+3+4+5+6+7 = 28

1+2+3+4+5+6-7 = 14

1+2+3+4+5-6+7 = 16

1+2+3+4+5-6-7 = 2

1+2+3+4-5+6+7 = 18

1+2+3+4-5+6-7 = 4

1+2+3+4-5-6+7 = 6

1+2+3+4-5-6-7 = -8

1+2+3-4+5+6+7 = 20

1+2+3-4+5+6-7 = 6

1+2+3-4+5-6+7 = 8

1+2+3-4+5-6-7 = -6

1+2+3-4-5+6+7 = 10

1+2+3-4-5+6-7 = -4

1+2+3-4-5-6+7 = -2

1+2+3-4-5-6-7 = -16

1+2-3+4+5+6+7 = 22

1+2-3+4+5+6-7 = 8

1+2-3+4+5-6+7 = 10

1+2-3+4+5-6-7 = -4

1+2-3+4-5+6+7 = 12

1+2-3+4-5+6-7 = -2

1+2-3+4-5-6+7 = 0

1+2-3+4-5-6-7 = -14

1+2-3-4+5+6+7 = 14

1+2-3-4+5+6-7 = 0

1+2-3-4+5-6+7 = 2

1+2-3-4+5-6-7 = -12

1+2-3-4-5+6+7 = 4

1+2-3-4-5+6-7 = -10

1+2-3-4-5-6+7 = -8

1+2-3-4-5-6-7 = -22

1-2-3-4-5-6-7 = -26

I thought of a reasonably simple solution, I'm not sure if anyone else also thought of it, I didn't read all the solutions, so I'm sorry if anyone had thought of this before me.

I  2  3  4  5  6  7 = 0 (frame of equation) **bold**

I added the last two digits and found that they equal 13. (6+7=13) So I tried and found that: 1-2-3-4-5 = -13 (negative 13), meaning that you simply need to add the last two digits to equal zero.

(1 - 2 - 3 - 4 - 5) + (6 +7) = 0.

This works because "-13" is the opposite integer of "+13" and opposite integers always add up to equal 0.

((1+2)-3)^(4+5+6+7)

yes!it is possible.

just simply thinking-----(1+2+....+7=28) and $\frac{28}{2}=14$

so, the number can be divided into two equal halves.so, we can make $14-14= 0$ in many ways.[using only +-]

Good god people, everyone does something unique while I just do this : 1 - 2 - 3 - 4 - 5 + 6 + 7

1-2+3+4-5+6-7=0

Maybe I was lucky, I got it on my second attempt using gut feel, lol. 1-2+3+4-5+6-7=0

This can be a solution: 1 + 2 - 3 - 4 + 5 + 6 - 7 = 0

If the series contains an odd number of odd numbers, that is, if it ends with $4n + 1$ or $4n + 2$ for a natural number $n$ , then the sum cannot be zero, because however the odd numbers are added or subtracted, the parity of their sum must be odd. For example, however you add or subtract two odd numbers, the resultant is even. However you add or subtract two even numbers, the resultant is even. However you add or subtract an odd number and an even number, the resultant is odd. If there is an odd number, say $2n + 1$ , of odd numbers, then we can pair them to obtain an even resultant, leaving only $1$ odd number remaining. The resultant for the $2n$ or $2n+1$ even numbers must be even as well. The total end result must therefore be odd. $$ If the series contains an even number of odd numbers, that is, if it ends with $4n + 3$ or $4n$ , then we can use the following algorithms.

Case of ending with $4n + 3$ :

$1 +(2 -3) +(-4 +5) +(6 -7) + \dots = 1 + n \cdot 1 + (n + 1) \cdot (-1) = 0$

Case of ending with $4n$ :

$(1 -2) +(-3 +4) +(5 -6) + (-7 +8) + \dots = n \cdot 1 + n \cdot (-1) = 0$

1-2+3+4-5+6=7

Since changing signs doesn't affect the parity of the number (odd or even), we add up the total to find 28. Since both 28 and 0 are even, their parities are equal and therefore the equation is possible.

The answer is Yes. Here's how: 1 - 2 - 3 - 4 - 5 + 6 + 7 = 0.

If there were an even number of pairs of numbers then the solution would write itself. 1+7=8, 2+6=8, 3+5=8 etc

In this case the solution won't work because there is an odd number of digits.

I noticed that 1+6-7=0 so we are left with 2+3+4+5 which IS an even number of pairs: 2+5 and 3+4

So the final solution is 1+2-3-4+5+6-7 or 1-2+3+4-5+6-7

1-2-3-4-5+6+7=0

1, 2 and 3 can easily sum to zero: 1 + 2 - 3 = 0. Then, pair the 4 & 5 to make 1, and the 6 & 7 to make -1, so those pairs cancel. Hence:

1 + 2 - 3 - 4 + 5 + 6 - 7 = 0

Also:

1 + 2 - 3 + 4 - 5 - 6 + 7 = 0

1+2=3, 3-3=0, 0-4=-4, -4+5=1, 1+6=7, 7-7=0. 1+2-3-4+5+6-7=0.

1+2-3-4+5+6-7=0

5+6=11

4+7=11

1+2=3

3=3

We can simply use a sum to cancel out the numbers:

1+2-3+4-5-6+7=0

1+2-3-4+5+6-7

The integers 1 to n will divide into 2 subsets the plus integers and the minus integers. The sum of these two subsets must be equal for the integers to sum to zero. Hence 1/2 x 1/2 x n(n+1) must be an even integer => n(n+1) = 4k (k an integer). This implies that n = 4m or 4m-1 for m = 1,2,3,4.... (all integers). Thus the zero sum can be obtained only for integers n = 0 (mod4) or n = 3 (mod4). these are 3,7,11,15... and 0,4,8,12,16....So only half of the integers are capable of the zero sum proposed. The way to get the assignment of + and - for the even group of integers is to mirror image around the mid-point (n/2) and stack the two groups so that 1 is above n, 2 is above n-1 and so on. Assign n/4 + and n/4 - over the n/2 columns to get the zero sum. For the odd integers group do the same mirror procedure on 1...n-1 then add or subtract n depending on the + and - assignment of the other integers.

1-2-3-4-5+6+7=0

First of all., the total of all the number comes to be 28. So, 14-14 helps us. Now the point which numbers to be added and which numbers to be subtracted arises. we can't subtract 1 right? so we need 13 more to add.., think of wch numbers can sum up to 13. yes u r right, its sum of 2, 5, 6 . That's it..,keep + infront of 2,5,and 6 and - in other places. Finally 1+2-3-4+5+6-7 = 0 .

Oh, come on Brian, don't be so dramatic! :) It can be visually seen very easily that 1+2-3-4+5+6-7 = 0 and 1+2-3+4-5-6+7 = 0 and ...

1+2-3+4-5-6+7=0

I used a simple approach, it's not as good as for example the subset that gets half way to the sum and then back again reasoning of Brian Charlesworth, but here it is:

First I noticed that 1 + 2 + 3 ... - 6 = 0, but it didn't help. Then that 1 + 2 - 3 ... = 0, which turned out to be more helpful. Subtraction is not commutative, but grouping as in this example (+1) + (-2) + (+3) + (+4) + (-5) + (-6) etc... is commutative, as used sometimes when rearranging formula in algebra in general.

Starting with the large and orcward pieces is a good rule for puzzles in general -7 +6 +5 -4 bingo, thats 0, the same as +1 +2 -3. I'll leave others to fill in the boxes above from the info in this paragraph.

Yes, because 1 – 2 + 3 + 4 – 5 + 6 – 7 = 0.

1-2-3-4-5+6+7=0

Following the story of Gauss's method here , I noticed that I could look for ways to add up the pairs of numbers to equal 7. For example

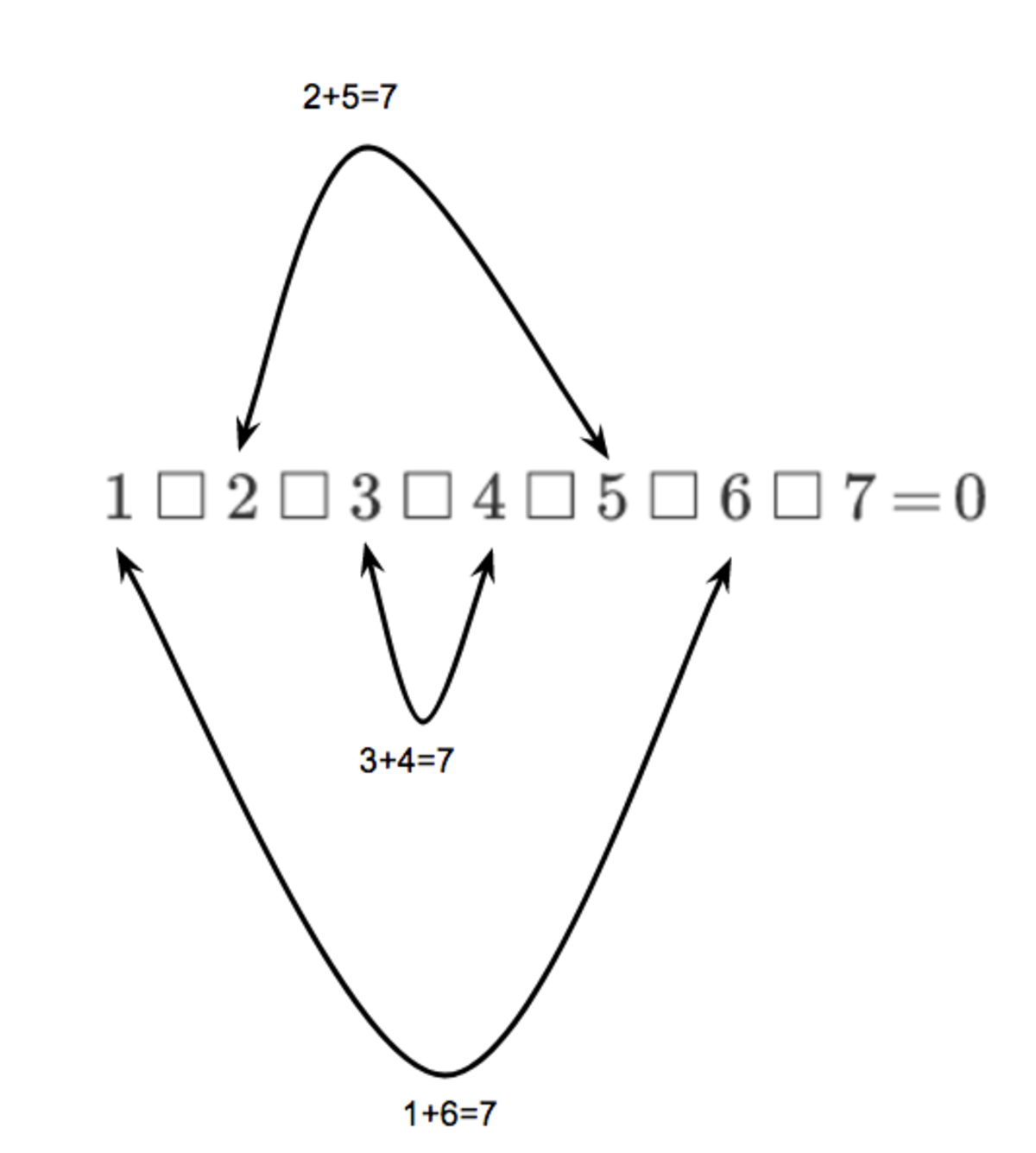
Since we have 2 pairs of 7's, we can easily choose our signs to ensure that they add to zero. This method should be able to help us easily know if the answer is 'yes' or 'no' for other values of n. If n is odd as in this example, we would need to ensure that there are an also an odd number of pairs (i.e. 2x3>>1,2,...,6 & 7; 2x5>>1,2,...,10 & 11, etc.) to add to the final number in the list. If n is even, we would need to ensure the opposite so that all values would match up (2x2>>1,2,3,4; 2x4>>1,2,...,8, etc.).

7+7-7-7=0 Three solutions possible with groups of seven.

This is where I have to eat very, very humble pie. Done on Excel, this takes less than a minute - but it's strictly trial and error, and offers no general method of solving such problems, so I will now defer to everyone who points out this is why 'proper maths' is (almost - there are a few things I won't give way on) always preferable to trial and error on a spreadsheet.

But probably not when you're teaching 9yo's

+1-2-3-4-5+6+7=0

because: 1+6-7=0 and 2-3-4+5=0 then: 1+2-3-4+5+6-7=0 Or: because: 3+4-7=0 and 1-2-5+6=0 then:1-2+3+4-5+6-7=0

One way This can be extended to any "4n or 4n-1" is by the following:

Each consecutive pair has a difference of 1 and therefore if we let one number be positive and one negative we get either +1 or -1 for the pair allowing us to create a useful pattern.

-1=-1,
+1-2=-1,
+1+2-3=0,
-1+2+3-4=0,
-1-2+3+4-5=-1,
+1-2-3+4+5-6=-1,
+1+2-3-4+5+6-7=0,
-1+2+3-4-5+6+7-8=0,
-1-2+3+4-5-6+7+8-9=-1

At any "n" we begin by alternating our signs in order from the largest number "n" being negative with "n-1" and "n-2" positive.. "n-3" and "n-4" negative and so on -> (...+,-,-,+,+,-) This pattern will yield 0 at every 3rd and 4th number. (I am cheating (using -1 wasn't in the original question) to make the pattern pretty but can still accomplish without using a negative before the one by inverting all signs)

A simple intuitive explanation of why it only happens at 3rd and 4th... every 4th number is even if you half it. 8/2=4 but 6/2=3. If we, like Gauss, take 24 and pair up its terms high with low 24+1=25, 23+2=25... we will have an even (12) pairs which can be opposed +/- to cancel out. Looking at 23, pair up 22+1=23, 21+2=23... for 11 pairs but add in the final 23 to get a total of twelve 23s which can all cancel. If you try this with 22 you only have eleven 23s and they would not fully cancel out but rather still have some remainder

Here the Que is

1<>2<>3<>4<>5<>6<>7=0

So now doing simple maths and some basic knowledge of addition and subtraction Than BIG methods ^_^

2<>3<>4<>5<>6<>7=-1 (subtracted 1 on both side)

Taking + - at different positions and hence got the answer

-2+3+4-5+6-7

No offenses​ to big methods just thinking more and remembering less

the numbers 1, 2, 3, 4, 5, 6, and 7 include four sets of seven (1+6=7, 2+5=7, 3+4=7, and 7) so two sets need to be positive and two sets need to be negative in order for the final solution to equal zero. Therefore any combinations with two groups of seven being negative and two being positive will result in a correct answer. Keep in mind that since 1 is positive, 6 must also be positive. Possible answers include 1-2+3+4-5+6-7=0 and 1-2-3-4-5+6+7=0.

1-2-3-4-5+6+7=0

1+2-3-4+5+6-7=1-(-2+3)+(-4+5)-(-6+7)=1-1+1-1=0. If n is 4q+3, q integer positive, then the solution is to alternate the sign in pairs after 1. The substraction of two consecutive numbers is 1 or - 1. The strategy is to alternative them. Similarly if n is 4q, in four in four the sign in pairs is alternsted +1-1. If n is 4q+1, or 4q+2, then the answeris not.

This is my solution:

1- 2 - 3 - 4 - 5 + 6 + 7 = 0

1- 2 - 3 - 4 - 5 = -13

6 + 7 = 13

-13 + 13 = 0

So yes it can be done!

Isnt the solution +-...-?

Simply find out groups of numbers cancelling each other. Eg: 7-(4+3)+6+1-(5+2)=0

This is very easy if you just stop and consider it a minute:

1) The sum of the numbers is 28 2) So you need to have numbers so that sum to half the total be preceded by a minus sign. 3) Since the FIRST digit will ALWAYS be positive (given the preconditions in the problem), you have to consider 2 general cases; when there is an odd number of terms, and when there is an even number of terms...

4) etc.

1-2-3-4-5+6+7=0

I Will use the property :1-a) Odd number of odd numbers when added or subtracted will always be odd.

1-b) Even number of odd numbers when added or subtracted will always be even.

1-c) Any number of even numbers when added or subtracted will always be even

2)Another property which will be used is that we can make any 4 consecutive integers sum to zero by using appropriate signs. If the 4 numbers are n, n+1, n+2, n+3 , We see that $+(n)-(n+1)-(n+2)+(n+3)=0$

3)Last property is 0 is the additive Identity 0 can be added or subtracted without changing the whole sum.

Let us begin with the proof:

If there are odd number of odd numbers then the answer will always be odd, irrespective of what signs we use. So for odd number of odds, getting sum 0 is impossible. (As 0 is an even number). This corresponds to cases that if there are $n$ terms and $n=4m-3$ or $n=4m-2$ we have odd number of odd numbers and thus getting sum 0 is impossible.

If $n=4m$ then Using the 2nd property, we can group them into $m$ groups of 4 consecutive integers. Thus, It can have sum 0.

If $n=4m-1$ , Here we shall 3rd property, Instead of considering numbers $1,2,...,n$ we shall consider $0,1,2,...,n$ This will have $4m$ terms and We can use 2nd property to get total sum 0.

Hence , we have proved that if $n=4m-3$ or $n=4m-2$ , It is always impossible to construct a sequence which has sum 0 and we have proved that if $n=4m-1$ or $n=4m$ , It is always possible to construct a sequence which has sum 0. Thus our proof is complete.

See it's too simple 1-2-3-4-5+6+7=0

1+2-3-4+5+6-7=0

Solution: 1+2-3+4-5-6+7=0 Answer to the Bonus question: We cannot generalize the solution. It depends whether the number of numbers is odd or even.

1-2-3-4-5+6+7=0 wat about this one? how wuld u generalise for nth series?

Yes. I found this sequence: 1 + 2 - 3 + 4 - 5 - 6 + 7 = 0. Indeed, a solution can be found for any n as long as sum (1,...,n) is even. This occurs when n = 4i or n = 4i-1, for i = 1, 2, 3, ... That is to say, when n = 3, 4, 7, 8, 11, 12, ...

1+2-3+4-5-6+7 = 0 1+2-3-4+5+6-7 = 0

Generalizing, Sum from k=1 to n n(n+1)/2 have to be even in order for 2,3,4...,n The elements sum: n(n+1)/4 which means the exercise can be satisfied for: n and n+1 if both of them mod 4 = 0

1 + 2 - 3 + 4 - 5 - 6 + 7 = 0

1 + 2 = 3, then 3 - 3 = 0, then 0 + 4 = 4, then 4 - 5 = -1, then -1 - 6 = -7, and -7 + 7 = 0.

Possible Solutions: 1-2-3-4-5+6+7=0, 1-2+3+4-5+6-7=0, 1+2-3-4+5+6-7=0, 1+2-3+4-5-6+7=0

1+2-3+4-5-6+7+=0

the answer : 1-2-3-4-5+6+7=0 (yes)

Is this possible to show the same for {1, 2, 3, 4, 5} ?