Plusplus area
A plus-plus is a polygon where all the side lengths are 1 and all the angles are right angles. The following two plus-plus polygons have areas 9 and 18, respectively. But not every integer can possibly be the area of a plus-plus.
Give the sum of all the impossible integers for the area of a plus-plus.
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The unit square is a plus-plus. A domino is not, nor are any tromino or tetromino. A "plus" shape of 5 squares is a plus-plus.
There are 4 fundamental ways to increase the size of a plus-plus.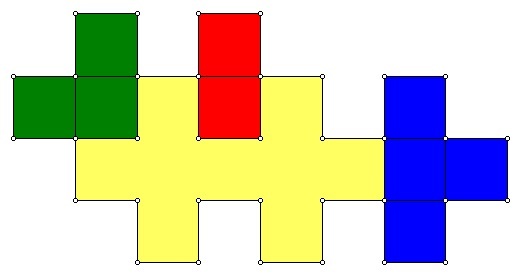
add 2 squares to turn a one-square concavity into an outward facing part. Shown in red, this requires a plus-plus with an inward divot to apply it. (The yellow shape with area 9 is the smallest one where this rule can be applied.)
add 3 squares to an inward corner. Shown in green. Every plus-plus except the unit square has at least one such inward corner.
add 4 squares to an outer edge. Shown in blue. Every plus-plus has at least 4 outer edges.
fill in a larger concavity. (Only applicable to large plus-plus.)
Once you have the area 5 you can easily increase this by 3 or 4, so 8 and 9 are possible as well as 11, 12, 13 and then every number beyond. The red rule can first be applied when the area is at least 9 so this doesn't help.
So the sum of impossibe areas is 2 + 3 + 4 + 6 + 7 + 1 0 = 3 2