Plusplus perimeter

Pretend that the sides of a plus-plus are traced by a moving point. This point moves one unit at a time, in any of the four standard directions.

Claim 1 : The number of horizontal moves = The number of vertical moves

This is because after the point moves horizontally, it must move vertically.

Claim 2 : The number of left moves = The number of right moves, and likewise for vertical moves.

This is because the point returns to where it starts. (Also, vertical moves don't affect horizontal displacement)

Claim 3 : Left moves = Right moves = Up moves = Down moves

Follows from the previous two claims.

Thus, the total number of moves is divisible by four, and 2018 clearly is not.

The unit square is a plus-plus with perimeter 4. There are 4 fundamental ways to change the perimeter of a plus-plus.

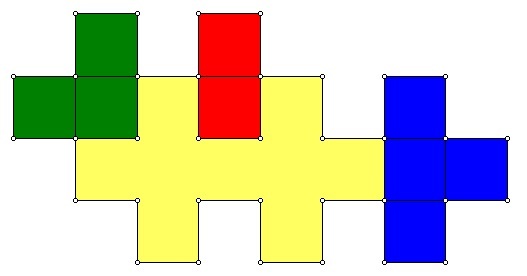
• add 2 squares to turn a one-square concavity into an outward facing part. Shown in red. This does not change the perimeter.

• add 3 squares to an inward corner. Shown in green. This increases the perimeter by 4.

• add 4 squares to an outer edge. Shown in blue. This increases the perimeter by 8.

• fill in a larger concavity. Like the blue rule, but this will decrease the perimeter by 4 or 8.

So the perimeter of a plus-plus will always be a multiple of 4. Since 2018 is not a multiple of 4, the answer is No .

Notice that any plus-plus can be changed (I think of it sides being pushed out) into a rectangular-esque shape, while still preserving the perimeter:

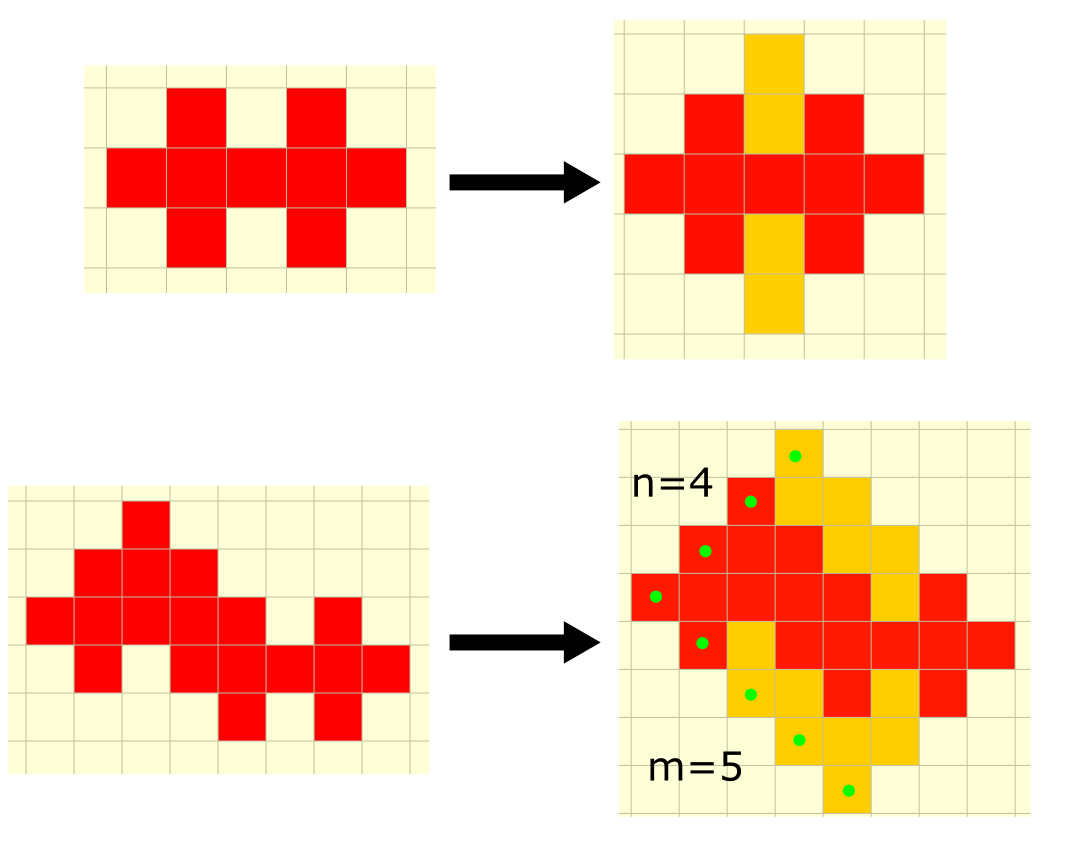
Call the number of squares along one side of this shape n , and the number of squares along the other side m . We can thus model an equation to find the perimeter of such a shape:

$p = 12 + 4(n - 2) + 4(m - 2)$

It is clear that the perimeter of any plus plus must be divisible by four, and as 2018 is not, there is no plus-plus with a perimeter of 2018 .

Prime factorization of 2018 is 2 and 1009. This shows that it will not be possible to satisfy the constraints of the problem.

For every side, there is one 90 degrees angle. For the shape to connect the number of (90 degrees) angles should be dividable by 4. perimeter 2018 means 2018 sides and thus 2018 angles. 2018 does not divide 4.

Imagine a checkerboard with squares of side 1. The external perimeter of a plus-plus must have the same colour squares adjacent to it on the outside (and the opposite colour inside). E.g. all the squares touching the perimeter of the shape by the side (not by a corner) are white, and all the internal squares touching the perimeter are black. This is true because the perimeter turns by 90 degrees which will go along another side of the same white square, or along a side of another white square.

So, we can think of the interior of the plus-plus as consisting of black and white squares, but none of the white squares are adjacent to the perimeter.

The perimeter of all the black squares taken individually is obviously a multiple of 4. This consists of the external perimeter of the plus-plus, as well as internal sides, each of which can be removed by filling in one of the white squares. Every time we fill in an internal white square we lose 4 units. Once we have filled in all the internal white squares we still have a multiple of 4.

In fact, if the plus-plus can be laid on a chess board covering B black squares and W white squares, then its perimeter is the absolute value of 4(B-W).

First divide the whole figure into two parts-the perimeter of First part corresponds to the first two digits(obviously,20)and that of 2nd corresponds to the last two digits(that is,1+1+1+.....32).So,when we read it together,since altogether it is a single plus plus polygon,we get 2032 instead of 2018. (Pardon me if my method is incorrect/inappropriate.I got it this way😊)

What if the shape is made such that when the shapes are joined, each only lose perimeter of 2??? Then it would be even???

In order to come back to the starting position you have to go up and left the same number of times as down and right respectively. So the total perimeter should always be a multiple of four, which 2018 is not.

No matter how big plus-plus that may be. It should be closed figure. To form a close figure the boundry should rotate exactly 360°. A clockwise rotation of 90° cancels a anti-clockwise 90° rotaion. That implies in any plus-plus polygon there should be 4 more rotation of any one kind than other. That means total rotation should be a integer multiple of 360°. This implies there should be exactly '4n' sides to the polygon. Where 'n' is any integer. 2018 is not multiple of 4. So answer is 'NO'

Clearly the first is a square (perimeter 4), the second a cross (perimeter 12), and from then on a new one increases the perimeter by four--this purely by experiment. I hypothesise that this continues indefinitely. As such, since 12 is dividable by four, then all plus-plus' from the cross (with perimeter 4) upwards in size, must also be divisible by four. 2018 is not divisible by 4, therefore no plus-plus exists with a perimeter of 2018.

* I can not visualise a plus-plus with a perimeter equal to eight--such as would be possible with some of the other solutions here. Can anyone enlighten me? *

In drawing the polygon, after every two sides drawn our pen moves in one of the following directions: $(1, 1), (1, -1), (-1, -1), (-1, 1)$ .

Let's say that the pen moved in these directions $a, b, c, d$ times respectively.

So the total number of double moves the pen made is $a + b + c + d$ .

After drawing the entire polygon, the pen must be back at the origin.

Therefore, $a(1, 1) + b(1, -1) + c(-1, -1) + d(-1, 1) = 0$ or equivalently $(a-c)(1, 1) + (b-d)(1, -1) = 0$ .

Since ${(1, 1), (1, -1)}$ are linearly independent, this only holds when $a-c=0$ and $b-d=0$ .

So the total number of double moves the pen made is $2a + 2b$ , an even number.

Thus the total number of single moves the pen made is divisible by 4, which excludes 2018.

The smallest plus-plus possible is actually a simple square, so its perimeter is 4 . The second one takes the shape of a "+" and its perimeter is $4 + 2 \cdot 4 = 12$

( 4 side lengths are reused and 2 are added for each sides).

The third one would be a "+" but with 3 more squares in one of the corners, so by the same way we get $12 + 2 \cdot 2$ , thus, its perimeter is 16 . This way we see that each figure is divisible by 4 . As 2018 isn't divisible by 4, there is no plus-plus with a perimeter of 2018.

This is my first comment and I'm French so please be indulgent with me ;)

I just did 2s+3s=2018 and couldn't solve for whole number?

This can be viewed as a wandering path problem, with some special constraints:

1. You must return to your point of origin. So for every move away from the origin you must eventually make a move back towards the origin.
2. Additionally, you must not retrace or cross your own path, therefore the final shape of your path will always describe a closed object - in this case a polygon because of the 1 unit / right angle constraints.
3. The shortest path is a square (4 steps).
4. Because of 1 thru 3, if you increase the number of points visited, it must always be by adding squares (4 steps).

Therefore the solution set is all positive integer multiples of 4 - which does not include 2018.

Stack the smaller plusplus of perimeter 20 with two another of same kind from above and below. Now its effective perimeter becomes 20-(7+7) which is 6.now repeat this with the stacked plusplus in both directions.So in order to achieve a plusplus with perimeter 2018 it must be divisible by 6, which is not the case here and hence not possible.

There is a pattern in the perimeters of the first three plus-plus polygons: 4 (unit square), 12 (plus sign), 20 (left, yellow figure on the problem). Notice that 4 = 4 x 1; 12 = 4 x 3; 20 = 4 x 5; which means that for a perimeter P we must find a whole number k {0, 1, 2, 3, 4 ...} satisfying P = 4 x (2k + 1). For P = 2018 there is no solution.

For it to be a plus plus the boundary along any given edge, regardless of complexity (top, bottom, left or right) must be an odd number of unit lines. Given this it logically follows that if any two are odd the other two cannot be and you therefore can't produce a valid plus plus shape.

I tried in a simple way.I found out the perimeter of the left part of the plus plus as well as the right part.They are the digits of a 4-digit no,since on the whole,they constitute a plus plus polygon,and I got the resulting perimeter as 2032,with 32 as the right side's perimeter.So,it is not 2018.