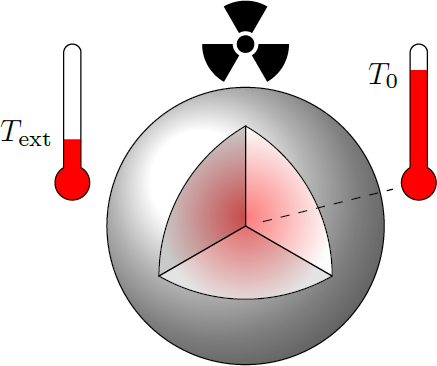
Plutonium hand warmer
Plutonium-238 produces a heat output of approximately 570 watts per kilogram by the nuclear decay.
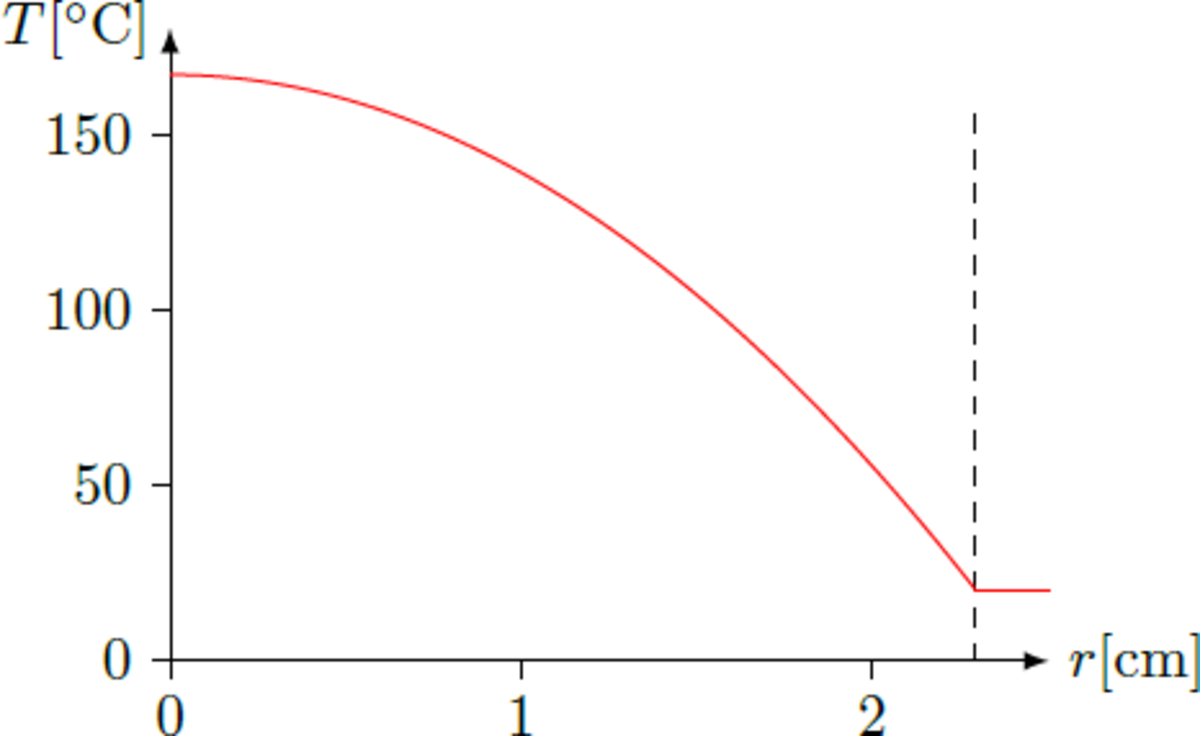
 What is the maximum temperature
inside a ball of plutonium with a mass of
in units of degree Celcius? (Round the result to the nearest integer.)
What is the maximum temperature
inside a ball of plutonium with a mass of
in units of degree Celcius? (Round the result to the nearest integer.)
Details and Assumptions:
- The stationary heat equation is in spherical coordinates where is the Laplace operator, is the heat conductivity, and is the heat power per volume.
- Plutonium has a density of .
- The surface temperature of the sphere is (ideal heat couple to the environment).
The answer is 167.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
A ball of mass m = 1 kg has a radius R , so that m = ρ ⋅ 3 4 π R 3 ⇒ R = 3 4 π ρ 3 m ≈ 2 . 2 9 cm The heat source density equals q ˙ ≈ 5 7 0 kg W ⋅ 1 9 , 8 0 0 m 3 kg ≈ 1 . 1 3 ⋅ 1 0 7 m 3 W The heat equation − λ Δ T ( r ) = − λ ( T ′ ′ ( r ) + r 2 T ′ ( r ) ) = q ˙ can be solved by T ( r ) = α r 2 + T 0 . Substitution in the differential equation yields ⇒ ⇒ ⇒ Δ T T ( r ) T ext T 0 = T ′ ′ ( r ) + r 2 T ′ ( r ) = 6 α = − λ q ˙ = − 6 λ q ˙ r 2 + T 0 = − 6 λ q ˙ R 2 + T 0 = T ext + 6 λ q ˙ R 2 ≈ 1 6 7 ∘ C