Point Symmetry Puzzle

The color of every square in the box is of immense significance for solving the problem correctly.

Let's figure out the option which satisfies the conditions of points symmetry about the origin which is "every part has a matching part at the same distance from origin but opposite in direction".

When we take the the option C into consideration, then we can visualize the image as follows:

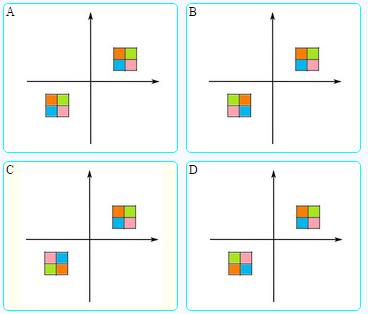So, the option C has point symmetry about the origin.

Simply diagonally swap the corners, since symmetry around the origin means flipping the object over the x AND y axis :)

If the figure is rotated clock wise by 180 degreesaround the origin only in case c we will get exactly the same image as before.

You can also think of the origin as a convex lens.

Starting from the centre equal distances on opposite sides should meet identical objects for point symmetry. Now one is convinced only C satisfies this.

In this case we do two times symmetric 1st time - 2nd coordinate (-x,y plane) 2nd time - 3rd coordinate (-x,-y plane) And we get this answer.

The symmetrical about origin can be correctly found by imagining the mirror across the origin. In option 'c' we can see the same colour I. e. Blue just in front of each other which other options doesn't have

I just applied simple tessellation from maths.

I got the correct answer, but this isn't a line of symmetry, or even a reflection. However it is a rotation.

So, can you have point symmetry and NOT have the same color in the position closest to the origin (assuming the squares are parallel to the vertices).

I mention this because I don't believe it is possible and with only one answer fitting that configuration, I was immediately drawn to that one rather than having to ascertain the correct answer by working through the problem

Colours of smaller squares is to be compared for symmetry

It is easy to ascertain the answer as symmetry is nothing but a mirror image and the option c exemplifies it with the green tile having the past opposite orientation