The Special Point In A Triangle 1

Geometry Level 5

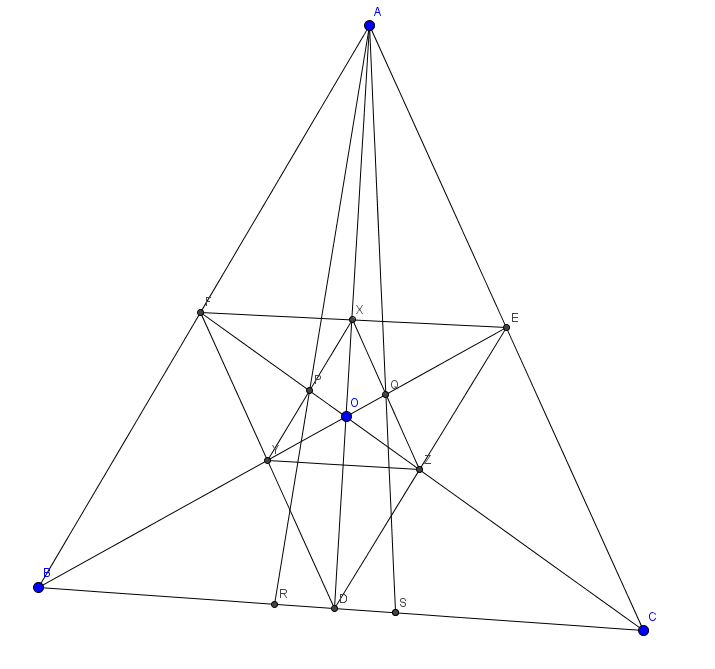
Let $O$ be a point in triangle $ABC$ .

$D$ is the intersection of $AO$ and $BC$ . $E,F$ are defined similarly.

$X$ is the intersection of $EF$ and $AD$ . $Y,Z$ are defined similarly.

Let $P$ be the intersection of $XY$ and $CF$ and $Q$ be the intersection of $XZ$ and $BE$ .

$R$ is the intersection of $AP$ with $BC$ and $S$ is the intersection of $AQ$ with $BC$ .

Find: $\dfrac{4 \times BS \times RC}{SC \times BR}$ .

The Special Point in A Triangle 2

The answer is 9.

1 solution

Sam Bealing
Mar 31, 2016

Solution using areal coordinates:

Let $A=(1,0,0),B=(0,1,0),C=(0,0,1),O=(l,m,n)$ then we have: $D=(0,m,n),E=(l,0,n),F=(l,m,0)$

The line $AD$ has equation $yn-mz=0$ and $EF$ has equation $-xnm+ynl+zlm=0$ . It follows that $X=(2l,m,n)$ is on both lines. Symettrically, we have $Y=(l,2m,n),Z=(l,m,2n)$ .

The line $XY$ has equation $-mnx-nly+3mlz=0$ and $CF$ has equation $-xm+yl=0$ . Again, $P=(3l,3m,2n)$ is on both of these lines. By symmetry, $Q=(3l,2m,3n)$ .

It follows then that $R=(0,3m,2n),S=(0,2m,3n)$ so $\frac{BR}{RC}=\frac{2n}{3m}$ and $\frac{BS}{SC}=\frac{3n}{2m}$ .

Therefore $\frac{4 \times BS \times RC}{SC \times BR}=4 \times \frac{RC}{BR} \times \frac{BS}{SC}=4 \times \frac{3m}{2n} \times \frac{3n}{2m}=9$

Moderator note:

Nice approach using barycentric coordinates.

Is there a reason why the final answer has such a nice form?

Nice approach using barycentric coordinates.

Is there a reason why the final answer has such a nice form?

Calvin Lin Staff - 5 years, 2 months ago

I am not really sure, I have looked for a synthetic approach but I haven't been able to find one yet.

Sam Bealing - 5 years, 2 months ago

Can we use projective geometry (parallel projection) to project the triangle to an equilateral triangle. Since ratios are preserved in parallel projectivity therefore the answer is also same for an equilateral triangle and we get the solution. Is it the right way. I don't know. I have just started reading projective geometry and I came across this problem so thought like this.

Jitarani Nayak - 3 years, 5 months ago

You can make ABC an equilaterial triangle. However, point O is still randomly chosen, so you will essentially have to go through the same calculations.

In this solution, you can see that's the first step.

Calvin Lin Staff - 3 years, 5 months ago

Yes, you are right. We can't choose O, even if it is a equilateral triangle. Thank you!!!

Jitarani Nayak - 3 years, 5 months ago

The Special Point In A Triangle 1

The answer is 9.

1 solution

Moderator note:

0 pending reports