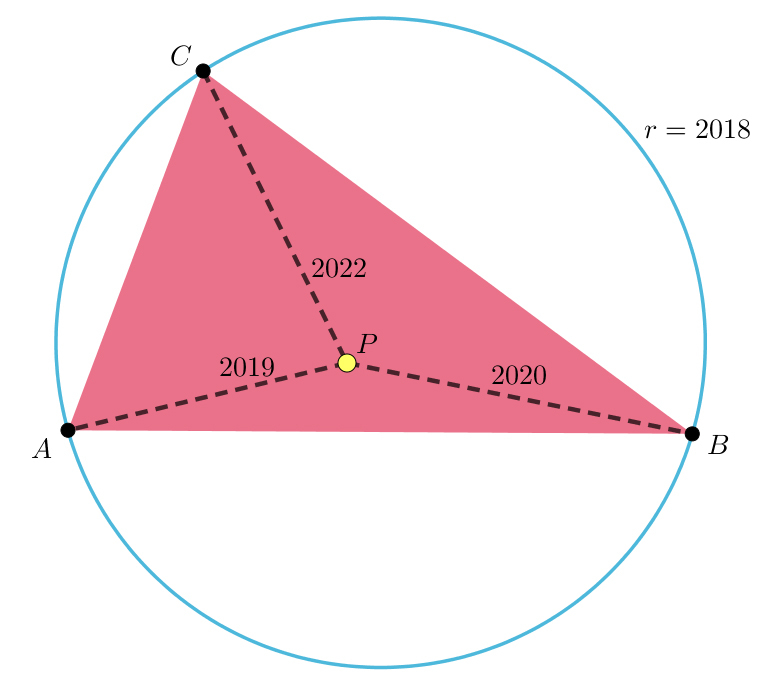
Point inside an acute triangle
The radius of the circumcircle of the acute triangle is .
Point is inside the triangle. Is it possible that ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Point P is very close to point O, the circumcenter, and intersection of the perpendicular bisectors of the sides, since the 3 distances given are virtually equal to each other, and traverse the distance from P to the circumference. If one assumes that P and O coincide, it is an ease matter to compute the triangke sides, which become 216.9, 153.4, and 190.6, with corresponding central angles of 3.08, 2.1, and 2.7, a long way from summing to 360. Ed Gray