Point square
Point P is inside square A B C D such that A P = 1 , B P = 2 , C P = 3 .
Find ∠ A P B in degrees.
The answer is 135.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
This certainly qualifies as "brilliant"!
In fact, the exact side length of the square is s = 5 + 2 2 (and the coordinates of P are ( 2 s s 2 − 3 , 1 − ( 2 s s 2 − 3 ) 2 ) ).
Sorry BP=2
very elegant, lovely solution!, just one question though, how do you assume that A, P and P' are co-linear
Log in to reply
A P and P' need not be co-linear; it has no bearing on the solution, but is a side-effect of the lines provided.
point A,P,P' aren't co-linear ,also the solution needn't them to be co-linear.
Thanks !^^
The vertices are incorrectly named (A, B, C, D clockwise rather than counterclockwise) Therefore, APB refers to a different angle.
Log in to reply
But isn't the angle generally represents angle which is obtuse or acute only? The angle of which bigger than 1 8 0 ∘ has a different name.
The question is wrong. It says BP=1. I got 138.6
Can you shed any light into how you came up with the elegant solution?
Log in to reply
Emmm, I have seen this kind of question before, which is a square and three given length. It always true and useful to know that rotate a triangle 90 degree and it can make the question become easier.
https://www.cut-the-knot.org/proofs/swivel.shtml
Mesmerising mathematics....👌
How do you know that angle CP'P = 90°?
Relevant wiki: Euclidean Geometry - Construction of additional points/lines
Nice job on providing the detailed figure.
Maybe you could improve your solution further by explaining what motivated you to do this construction.
You have a nice proof. The preceding proof is not a proof at all.
Good one, except that right from the beginning you left us wondering what in the world is P' In other words, you constructed point P' without first explaining how.
I like this one. Wish I had thought of it. I used coordinate geometry: Point P has coordinates x,y.
( 1 ) x 2 + y 2 = 1
( 2 ) ( s − x ) 2 + y 2 = 4
( 2 ) ( s − x ) 2 + ( s − y ) 2 = 9
2 s s 2 − 3 = x combining 1 & 2
2 s s 2 − 5 = y combining 2&3
( 2 s s 2 − 3 ) 2 + ( 2 s s 2 − 5 ) 2 = 1
s 4 − 1 0 s 2 + 1 7 = 0
s 4 − 1 0 s 2 + 2 5 = 8
( s 2 − 5 ) 2 = 8
s 2 − 5 = ± 2 2
s 2 = 5 ± 2
Law of cosines
5 + 2 2 = 5 − 2 ∗ 2 cos θ
4 cos θ = − 2 2
cos θ = − 2 2
θ = 1 3 5 ∘ (215 does not work for triangles)
Relevant wiki: Cosine Rule (Law of Cosines)
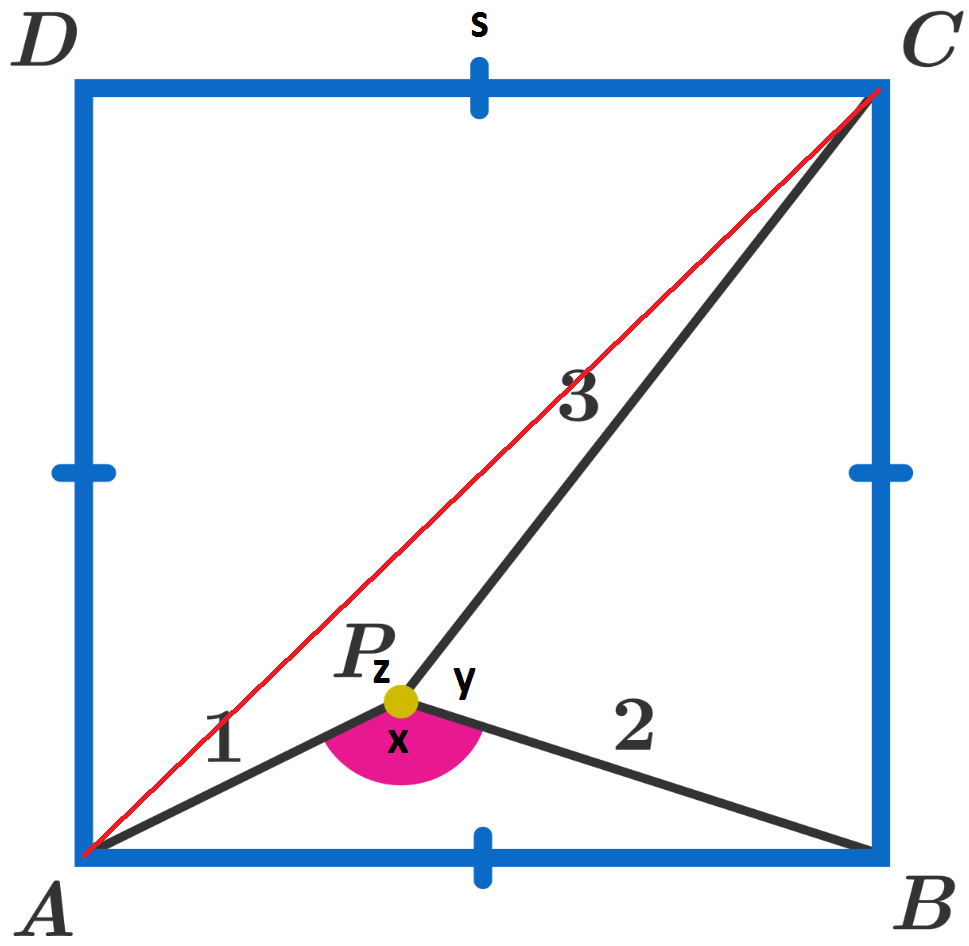
For simplicity let us label the side of the square 's' and the angles APB, BPC, CPA as 'x', 'y', and 'z' respectively.
Connect A to C to form another triangle APC. The length of this line is s 2 .
We can now form the following four equations,
( 1 ) x + y + z = 2 π
( 2 ) s 2 = 5 − 4 c o s ( x )
( 3 ) s 2 = 1 3 − 1 2 c o s ( y )
( 4 ) s 2 = 5 − 3 c o s ( z )
Next, as all are equal to s 2 we can re-arrange (3) and (4) in terms of x to get;
( 5 ) y = c o s − 1 ( ( 2 + c o s ( x ) ) / 3 )
( 6 ) z = c o s − 1 ( 4 c o s ( x ) / 3 )
Now we can substitute (5) and (6) into (1).
x + c o s − 1 ( ( 2 + c o s ( x ) ) / 3 ) + c o s − 1 ( 4 c o s ( x ) / 3 ) = 2 π
I then used Wolfram Alpha to plot this. You will find there are two solutions; 7 π / 4 and 3 π / 4 (aka 3 1 5 ∘ and 1 3 5 ∘ ). The only one that makes sense is 1 3 5 ∘ .
I'm glad to know I wasn't the only one who didn't came up with an elegant demonstration and had to use a brute force approach 😂
can you please explain how you got Y and Z in terms of X? I got lost at that transformation.
Brute force and ignorance solution: Call the side of the square x Then use cosine rule to find Cos x in triangle APB and Cos (90-x) in triangle CPB
So we will find x = sq root (5 + 2 root2) and Cos APB = (5 - (5 + 2 root 2))/4 = - 1/root 2. Hence 135 deg
Where do all you clever people get the mathematical symbols?
You asked about math symbols. They come from "unicode", the successor to "ASCII", which is well supported by most browsers these days. https://unicode-table.com/en/#221A has a table of all unicode (including characters for almost every language known to man) You want the square root, unicode hex 0x221A which displays as √, and maybe the degree symbol, 0xB0 which displays as °. How to enter these symbols depends on your operating systems https://en.wikipedia.org/wiki/Help:Entering special characters#Keyboard_code , but most browers support copy-paste (search for "Unicode" and the name of the symbol you want or search "unicode math") from a page listing convenient symbols.
135°.
Let the side of the square be a, and the
coordinates of point P be (x, y).
We have,
x^2+y^2 = 1,
(a-x)^2+y^2 = 4,
(a-x)^2+(a-y)^2 = 9
Subtracting 2nd equation from 3rd gives,
a^2-2ay = 5,
ay = (a^2 - 5)/2...........(I).
Applying cosine law in triangle APD gives,
a^2 = 1 + 4 - 4cosP,
=> cosP=(5 - a^2)/4
Substituting from (I) above gives,.
cosP = - (ay)/2,
Applying sine law gives,
sinP/a = sinA/2,
But sinA = y/1,
=> sinP = ay/2,
Therefore, tanP = sinP/cosP = -1,
So, P = 135°.
Let Coords of p = x,y
Let the length of segment of square be a.
In the first triangle, X^2+y^2 = 1 Y^2 = 1-x^2
In the second triangle, Y^2 + (a-x)^2 = 2^2
1-x^2+(a-x)^2 = 4
1-x^2 + a^2-2ax + x^2 = 4
A^2-2ax = 3….(1)
In the third triangle, (a-x)^2+(a-y)^2 = 3^2
(a-x)^2+(a-y)^2 = 9…(2)
Y^2+(a-x)^2 = 4 ….(3)
Subtracting 3) from 2), we get (a-y)^2 – y^2 = 5
A^2-2ay = 5…(4)
Dividing 4) by 1) and simplifying , we get (a-2y) / (a-2x) = 5/3
3a-6y=5a-10x
10x-6y=2a
a=(10x-6y)/2 = 5x-3y
Substituting the above in the expression (a-x)^2 + y^2 = 4, we get
(4x-3y)^2 + y^2 = 4
16x^2-24xy + 9(1-x^2) + 1—x^2 = 4
6x^2-24xy = -6
6x(x-4y)=-6
X(x-4y)=-1
x-4y=-1/x
y=(x+1/x)/4
y^2=(x+1/x)^2/16
= (x^2+2+1/x^2) / 16
= (x^4 + 2x^2+1 )/ 16x^2
Substituting in x^2 + y^2 = 1 and simplifying, we get 16x^4 + x^4 + 2x^2 + 1 = 16x^2
17x^4 + - 14x^2 + 1 = 0,
It would seem that this is a quadratic in x^2 but the solutions obtained by the usual formula yield wrong values We apply Newton Raphson method to the above equation with an initial value of 0.75. For some reason, initial values <= 0.5 seem to yield wrong results
X 0.862856209
Y 0.505449465
A 2.797932652
a^2 7.828427125
We apply cosine rule of triangles to get ,
Cos(APB) = [a^2-(1+2^2)]/-(212)
= 2.828427 / -4
= -0.70711
APB = arccos(-0.70711)
= 2.356194 in radians = 135 in degrees
FAKE question, You changed the lettering of the large square.
The eggheads approach. It must be a rational multiple of 180 degrees, else the desired solution would have lots of dp. And it's visually 135 rather than 120 or 150. So we guess 135. And it is!! I know this approach wouldn't win a Cambridge Tripos, but so what!
I don't get it. 135 is not a multiple of 180... Neither is 120 or 150. 0.o
Connect point A to point C so angle (cab)=45° ,put square side k,cos(cap)=(1+2k^2-9)÷(2×1×√2k),cos(bap)=(1+k^2--4)÷(2×1×k) as per the figure angle (bap)=45-(cap) so cos(bap)=cos45×cos(cap)-sin45×sin(-cap). so (k^2-3)÷(2k)=(1÷√2)×((k^2-4)÷(√2k))+(1÷√2)×((1-(k^2-4)^2÷√k))^.5 by brief the equation (k^2-3)=(k^2-4)+√(2k^2-(k^2-4)^2) so √(2k^2-(k^2-4)^2)=1 by square two terms k^4-10k^2+17=0 so k^2=5+√8 OR 5-√8 by substitute k values resulting that the right value is √(5+√8) , so @∆ BPA cos(bpa)=(1+4-(5+√8))÷(2×1×2)=-√8÷4=-1÷√2 so the required angle =135°#######
Relevant wiki: Euclidean Geometry - Construction of additional points/lines
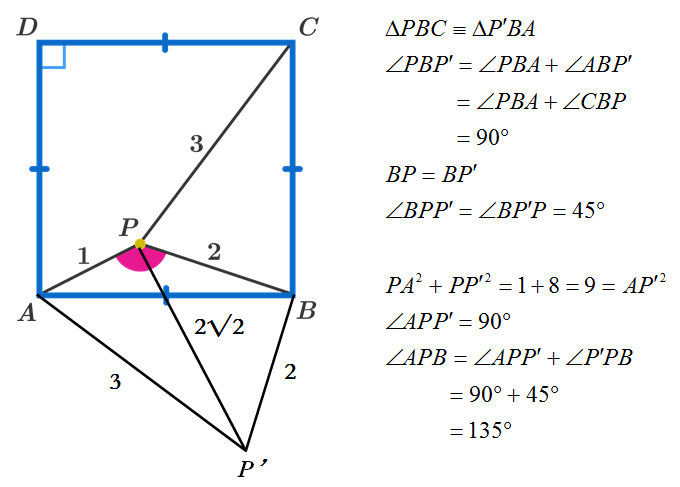
First we rotate triangle A B P clockwise 9 0 ∘ , to form a new point P ′ , then connect P ′ P .
Triangle P B P ′ form a isosceles triangle, and it is easy to know ∠ P B P ′ = 9 0 ∘ , ∠ B P ′ P = 4 5 ∘ so P ′ P = 8 .
Wait! Coincidentally, 3 2 = 8 2 + 1 2 , P C 2 = P ′ P 2 + P ′ C 2 .
So, ∠ P P ′ C = 9 0 ∘
As what the question ask for, ∠ A P B = ∠ C P ′ B = ∠ B P ′ P + ∠ P P ′ C = 1 3 5 ∘