Pointless Circles
An infinite triangular lattice consists of points spaced 1 unit apart.
What is the probability (as a percentage) that a circle of unit diameter placed randomly in the lattice encloses no lattice points, as shown?
The answer is 9.3100317883.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The problem should say how many significant figures are required.
Log in to reply
It is my understanding that Brilliant software takes anything within 2% of the correct answer as correct.
I think the math checks out and everything. But I can't wrap my head around the idea that: if you let a ring (the circle) fall onto this lattice there are just countable infinity possible ways in which the ring falls exactly between those gaps but uncountable many possibilities for it to enclose the ring (think of a gridpoint inside the ring and then you can move the circle quite a bit). So it seems like the probability of getting a natural number out of a random number generator that puts out random real numbers.
Log in to reply
The number of points the circle can fall on and not surround any lattice points is uncountably infinite. Just like you can move around the circle and the point will stay inside the circle, you can move the center of the circle around in the yellow section and all points will stay outside the circle.
While I did solve it exactly like you did, this problem reminds me of the Bertrand's paradox, where the "placed randomly" is not enough to completely specify the problem. There are many ways of placing randomly, and uniform distributions will lead to different results on different coordinate systems.
unfortunate, the first time, I found the area of the small triangle created by linking all midpoints of the arcs in decimal form, next time, I turned it to percentage, third time, I got the 3 1/3 circle area answer but i forgot to divide the area by root 3/4 or the area of the triangle, rip
In the 2nd line, must it not be : "within a distance of 1/2 from a vertex" ?
After connecting the lattice grid, the circle's center must be in an equilateral triangle. Since the circle has radius 2 1 , this center must be more than 2 1 away from any of the vertices of the triangle. The region in which this is true can be found by constructing three circles of radius 2 1 around the three vertices:
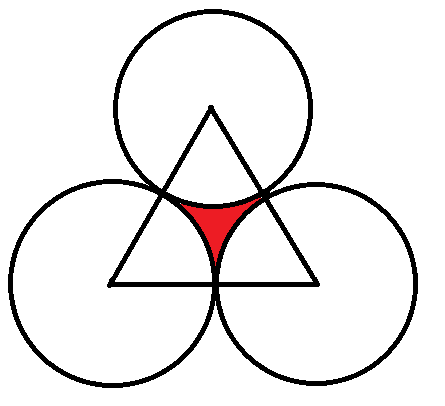
The area of the equilateral triangle is 4 3 . The area of each sector in the triangle is 2 1 ( 3 π ) ( 2 1 ) 2 = 2 4 π . Therefore, the probability is 4 3 4 3 − 3 ( 2 4 π ) = 1 − 2 3 π ≈ 9 . 3 1 %
How did you get root 3 over 4?
Log in to reply
The area of a triangle with side length s is 4 s 2 3 . This is derived by using Pythagorean Theorem to find the triangle's height.
What does a lattice point mean???
Log in to reply
They are a set of infinite equally-spaced points on a plane. Often when we consider lattice points, we think of the integer coordinates on the xy-plane since these are all exactly one unit apart from each other. The difference in this problem is that after connecting all these points, instead of ending with squares, we end with triangles.
The picture is misleading. From what it looks, there's only one point in each triangle that can contain a unit circle, so the obvious answer is a limit at 0 probability. You have to see through it to actually find the task at hand.
Log in to reply
What are you talking about? The answer that you said is right and wrong
The picture shows a gap between the circle and lattice points, implying that the circle can be moved around without touching the lattice points. In that case, the probability does not approach 0.
Within each triangle those circles with a center within distance 1 of a vertex, that is within the orange pie slice, will contain a point. Those with a center within the yellow region will not.
So the problem is to find the percentage of the area that is yellow.
To do that take the area of the triangle, 4 3 , and subtract from it the area of the tree pie slices which is equal to half a circle with radius 2 1 , that is 8 π .
Divide the result by area of triangle 4 3 and you get 2 3 2 3 − π = 0 . 0 9 3 1 = 9 . 3 1 percent