This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Connecting B and D creates a right triangle with BD the hypotenuse. The length of BD is then 5, being a 3-4-5 right triangle. The angle at C can be found using the law of cosines: 5 2 = 1 3 2 + 1 2 2 − 2 ( 1 2 ) 1 3 c o s ( C ) , therefore C = a r c c o s ( − 3 1 2 2 5 − 1 4 4 − 1 6 9 ) = a r c c o s ( 1 3 1 2 ) = 2 2 . 6 1 9 8 6 4 9 5 o . The semiperimeter: s = 2 4 + 3 + 1 3 + 1 2 = 1 6 . Using Bretschneider's Formula the area of the quadrilateral can be found to be: ( 1 6 − 1 3 ) ( 1 6 − 1 2 ) ( 1 6 − 4 ) ( 1 6 − 3 ) − 1 3 ( 1 2 ) 4 ( 3 ) c o s 2 ( . 5 ( 9 0 o + 2 2 . 6 1 9 8 6 4 9 5 o ) ) = 1 8 7 2 − 1 8 7 2 c o s 2 ( 5 6 . 3 0 9 9 3 2 4 7 ) = 1 2 9 6 = 3 6
I was unable to find suitable methods of simplifying the cos(.5(90+arccos(12/13)) by hand, and as such had to resort to a calculator. If anyone can offer insght - maybe using a power series approximation?
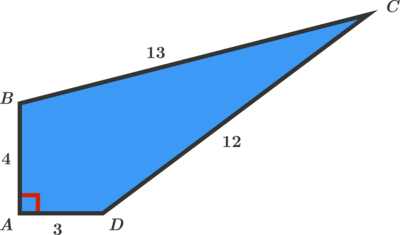
Also 1 3 2 = 1 2 2 + 5 2 ⟹ ∠ B D C = 9 0 ∘
[ A B C D ] = [ A B D ] + [ B C D ] = 2 1 × 3 × 4 + 2 1 × 1 2 × 5 = 6 + 3 0 = 3 6