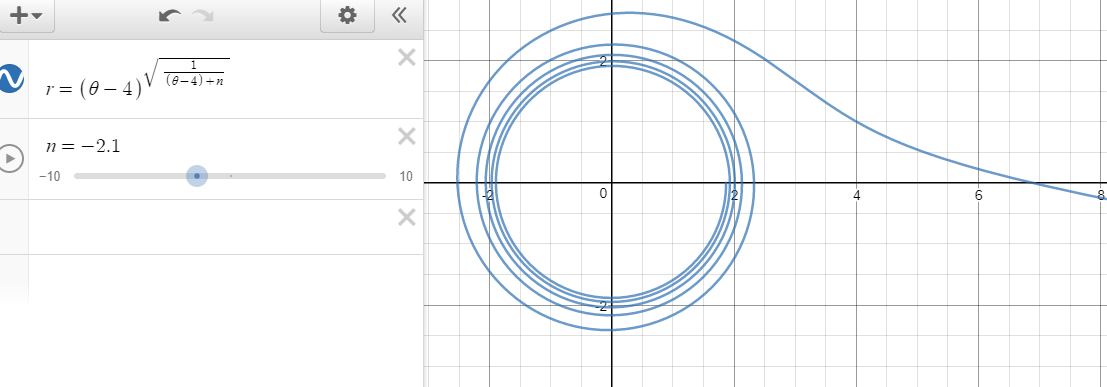
Polar Equation: Convergence

Algebra Level 4

What is the maximum value of $n$ that causes the graph of the polar equation below to converge for $0 \leq \theta \leq 10\pi?$

Note: A graph converges if it can be bounded by a circle with finite perimeter for a given domain.

-2

-1

\pi-4

0

1

\pi

1 solution

Timothy Cao
Apr 1, 2018

[Amateur's explanation]

Consider the Cartesian version of this polar equation: (easier to type)

$y = (x-4)^{\sqrt{\frac{1}{(x-4)+n}}}$

This is an equivalent function

$y = e^{ln(x-4) (\frac{1}{(x-4)+n})}$

We can simply find when the exponent that is $ln(x-4) (\frac{1}{(x-4)+n})$ diverges to positive infinity

(If it diverges to negative infinity, the entire power goes to 0)

Considering the bounds $0 \leq \theta \leq 10\pi$ ,

The above expression only diverges to positive infinity while $(x-4) < -1$

Note: We ignore the restriction from the ln because we created that restriction