Polarization experiment with mircowaves
A transmitter and a receiver for microwaves are placed opposite each other along the -axis, so that maximum reception is ensured. Now, a grid frame of metallic wires is placed between the transmitter and receiver, so that the wires enclose an angle of with the -axis. What is the radiation intensity measured at the receiver? Give the result relative to the original intensity measured without wire mesh.
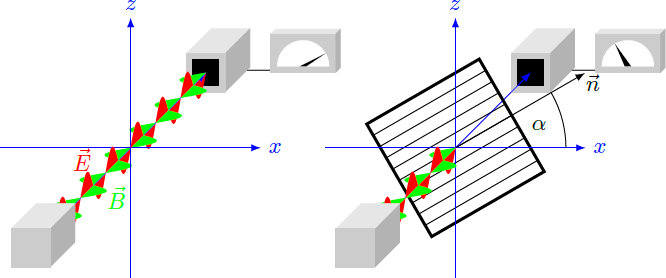
Details and Assumptions: The transmitter generates microwaves that are linearly polarized along the -axis. The receiver is identical to the transmitter and receives only the linearly polarized portion of the radiation. The wavelength of the microwaves is significantly larger than the wire spacing of the metal grid.
The answer is 0.125.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The metal grid acts as an polarizer for the microwave.
If the metal grid is at an angle of α = 0 ∘ to the x-axis, the electric field of the wave and the grid bars are perpendicular to each other, so that no current flow is caused in the metal. In this case, the the wave passes undisturbed through the grating and an intensity of I = I 0 is measured by the receiver.
However, if the angle is α = 9 0 ∘ , electrical voltage is caused along the metal wires by the electric field of the microwave. This leads to an alternating current in the metal whose current strength just compensates for the external voltage. The electric field on the side of the receiver therefore yields zero, so that the grating here acts as a mirror, at which the wave is completely reflected. Therefore, the measured intensity results I = 0 .
Otherwise, the electric field can be separated in components parallel and perpendicular to the grid bars: E = E ∥ n + E ⊥ t = E sin α ⋅ n + E cos α ⋅ t with unit vectors n and t with ∣ n ∣ = ∣ t ∣ = 1 , n ⊥ t . Only the tangential component of the wave passes through the grid, so that the electric field behind the grid results E ′ = E cos α ⋅ t The receiver also acts as a polarizer and registers only the component parallel to the z-axis. The electric field is separated into E ′ = E x ′ e x + E z ′ e z = E ′ sin α ⋅ e x + E ′ cos α ⋅ e z The received electrical field therefore gives E ′ ′ = E ′ cos α ⋅ e z = E ( cos α ) 2 e z Therefore, the received intensity results I ⇒ I = 2 1 c ε 0 ∣ E ′ ′ ∣ 2 ∝ ∣ E ′ ′ ∣ 2 = ( cos α ) 4 I 0 = 2 4 1 I 0 = 0 . 1 2 5 ⋅ I 0