Pole Malone
There are two telephone poles, each is
high and they are
apart. However the mechanic messed up and connected them by a cable, that is
long.
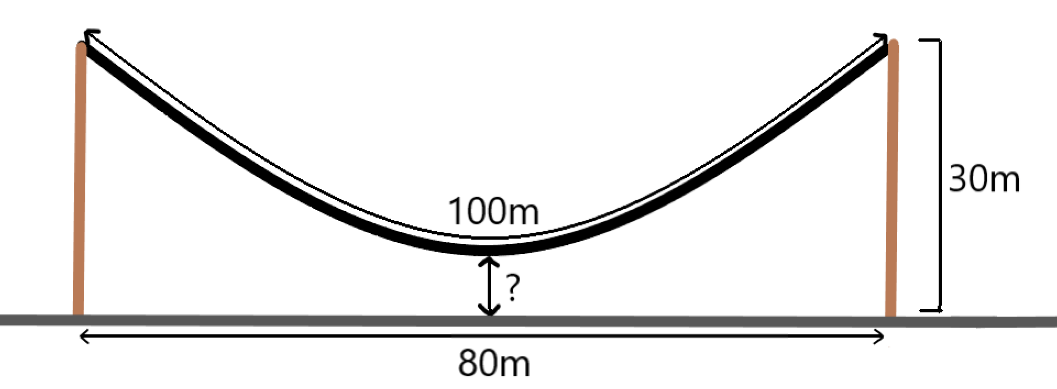 What is the distance from the lowest point of the cable to the ground in meters?
What is the distance from the lowest point of the cable to the ground in meters?
Note: A chain or a rope attached to two fixed points bends under its own weight. The resulting form can be described with the function .
The answer is 3.46.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The arclength of the catenary is S i n h ( x ) , so first we solve for x 0 in
S i n h ( x 0 ) = 4 0 5 0 x 0
which numerically works out to x 0 = 1 . 1 8 2 7 2 5 5 3 9 8 . . .
Then, a = x 0 4 0 , and we have the equation for the catenary that passes through ( − 4 0 , 3 0 ) and ( 4 0 , 3 0 )
f a ( x ) = 2 a ( e − a x + e − a x ) − 2 a ( e − x 0 + e x 0 ) + 3 0
so that at x = 0 , the wire is
a − 2 a ( e − x 0 + e x 0 ) + 3 0 = 3 . 4 5 6 2 4 9 0 8 5 8 . . .
above the ground