Polka Dots in Pi

Area of Yellow region,

$\begin{aligned} & =\frac{1}{6}\cdot \frac{\pi a^2}{4}-\frac{1}{2} \cdot \sin 60^\circ \cdot \frac{a^2}{4} \\ & =\frac{a^2}{8}\left( \frac{\pi}{3}-\frac{\sqrt{3}}{2}\right) \end{aligned}$

Area of 1 red region = Sector PHQ - 2 Yellow regions.

$\begin{aligned} & = \frac{1}{6} \cdot \frac{\pi a^2}{4} -2\left( \frac{a^2}{8}\left( \frac{\pi}{3}-\frac{\sqrt{3}}{2}\right) \right) \\ & = \frac{1}{24}\pi a^2 -\frac{1}{12} \pi a^2 +\frac{\sqrt{3}}{8} a^2 \\ & = \frac{\sqrt{3}}{8}-\frac{1}{24}\pi a^2 \\ & = \frac{a^2}{8}\left(\sqrt{3}-\frac{\pi}{3}\right )\end{aligned}$

So the total red area,

$=2\cdot \frac{a^2}{8}\left(\sqrt{3}-\frac{\pi}{3}\right) = \frac{a^2}{4}\left(\sqrt{3}-\frac{\pi}{3}\right ) \\ \Rightarrow \frac{4\cdot 3}{3} =\boxed{4}$

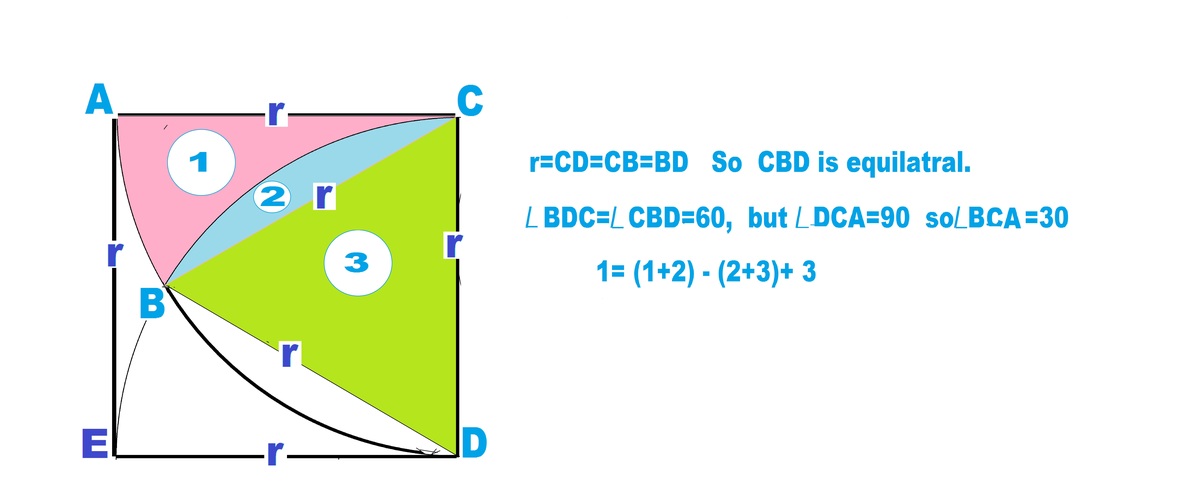
$\text{Consider one fourth of the square as shown in the sketch. It is a square with sides a = 2r.}\\ \text{The quarter circles ABD and CBE are with radii r.}\\ \therefore r = CD = CB = BD. ~ \implies~ CBD~ is ~an ~ equvilateral~\Delta.\\ \implies \angle BDC=\angle DCB=60~, but ~\angle DCA=90,~~ \therefore ~ \angle BCA=30.\\ \text{Areas~~ 1=(1+2) - (2+3) + 3 }\\ Area ~ 1+2=\dfrac{\pi*r^2*30}{360},~~~Area ~ 2 + 3=\dfrac{\pi*r^2*60}{360},~~~Area ~ 3=\dfrac{\sqrt3*r^2} 4.\\ \therefore~Area ~1=\dfrac{\pi*r^2*30}{360} - \dfrac{\pi*r^2*60}{360} +\dfrac{\sqrt3*r^2} 4=\dfrac{\sqrt3*r^2} 4 - \dfrac{\pi*r^2*30}{360}.\\ Total ~Red ~ area~from ~given ~diagram ~=4*\{\dfrac{\sqrt3*(\frac a 2)^2} 4- \dfrac{\pi*(\frac a 2)^2}{12}.\}\\ \dfrac{a^2} 4*(\sqrt3- \dfrac \pi 3), ~~~\dfrac{4*3} 3=\Large ~~\color{#D61F06}{4}$