Poll results
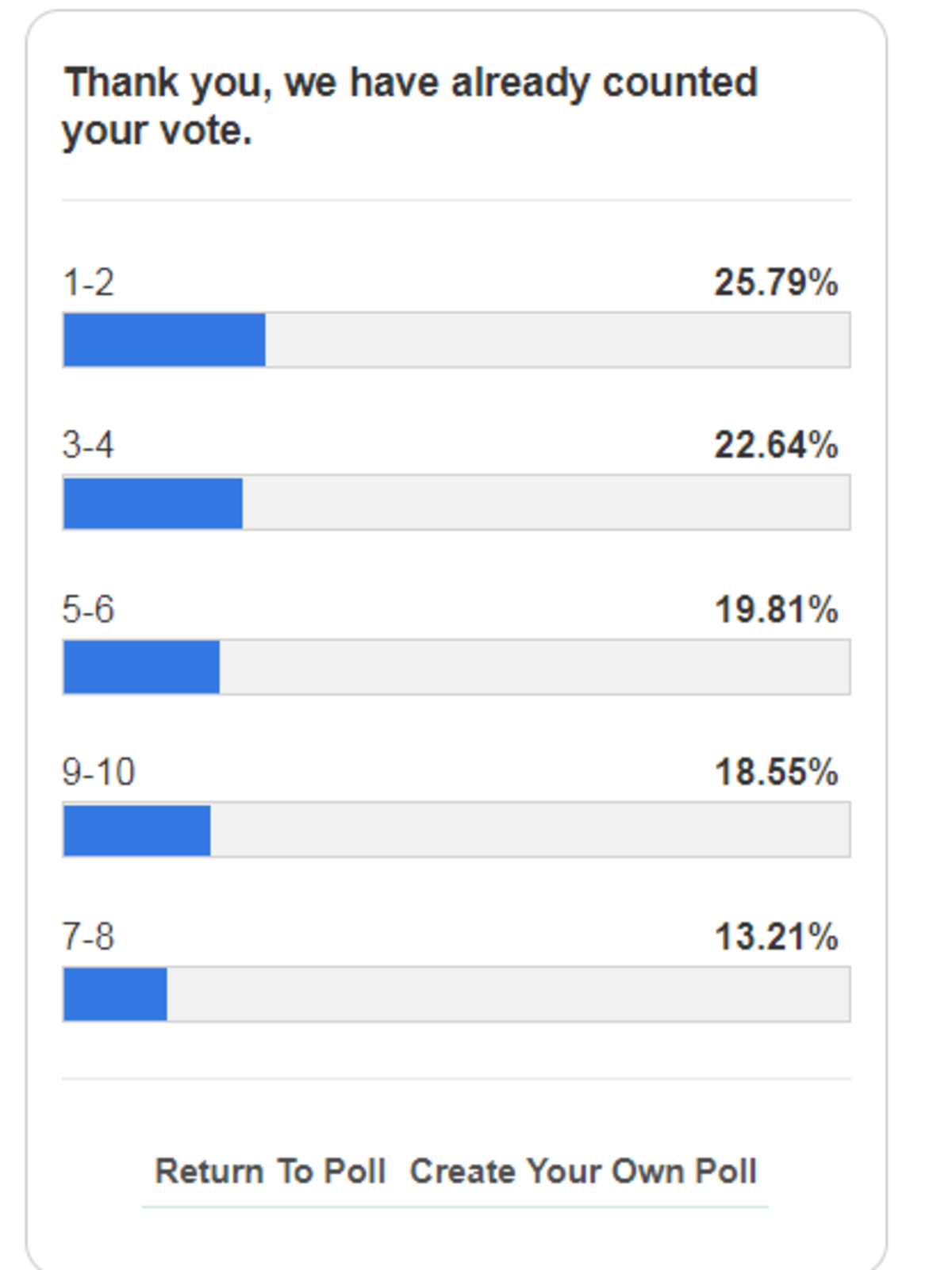
Given the distribution of votes above, with each option's percentage being rounded to 2 decimal places, what is the minimum number of people who could've taken part in the poll?
For example, it's possible people took part in the poll, with option 1-2 having votes, 3-4 - votes, 5-6 - votes, 9-10 - votes and 7-8 - votes. This is, however, not the minimum number of part takers.
The answer is 318.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The following technique is used in chemistry to derive an empirical formula based on given percentages.
First, divide each of the percentages by the smallest percentage. With some luck, we may recognize simple-number ratios. 2 5 . 7 9 ÷ 1 3 . 2 1 2 2 . 6 4 ÷ 1 3 . 2 1 1 9 . 8 1 ÷ 1 3 . 2 1 1 8 . 5 5 ÷ 1 3 . 2 1 1 3 . 2 1 ÷ 1 3 . 2 1 = 1 . 9 5 2 3 1 = 1 . 7 1 3 8 5 = 1 . 4 9 9 6 2 = 1 . 4 0 4 2 4 = 1 . 0 0 0 0 0 ≈ 1 7 5 ≈ 1 2 1 = 1 If the number of votes is not too large, the fractions on the right should be exact. This means that the number of people who voted for "7-8" must be a multiple of 14. We multiply all ratios by 14 and see what happens: 1 4 × 1 . 9 5 2 3 1 1 4 × 1 . 7 1 3 8 5 1 4 × 1 . 4 9 9 6 2 1 4 × 1 . 4 0 4 2 4 1 4 × 1 = 2 7 . 3 3 2 3 = 2 3 . 9 9 3 9 = 2 0 . 9 9 4 7 = 1 9 . 6 5 9 3 = 1 4 . 0 0 0 0 ≈ 2 7 3 1 ≈ 2 4 ≈ 2 1 ≈ 1 9 3 2 = 1 4 Again, we multiply by the common denominator 3 and find the numbers 8 2 , 7 2 , 6 3 , 5 9 , 4 2 for a total of 3 1 8 . It is not difficult to check that the fractions 8 2 / 3 1 8 , 7 2 / 3 1 8 , etc. indeed correspond to the given percentages.
Brute force method
Output: