Poly Bridge

As an example, consider the balance of forces at the point $A$ . Along the connecting elements act the forces $\vec f_ {AB}$ and $\vec f_ {AD}$ , which must add to zero with the outer force $\vec F_A$ . Geometrically, this means that the vector arrows correspond to the sides of a right-angled triangle of forces. Since the force $F_A$ corresponds to the leg opposed to $\alpha$ , it follows $f_ {AB} = F_A / \tan \alpha$ for the other leg and $f_ {AD} = F_A / \sin \alpha$ for the hypotenuse.

Calculating the balance of forces for all other points, the following forces finally result: $\begin{aligned} f_{AB} &= f_{BC} = - \frac{1}{2 \tan \alpha} F_B \\ f_{AC} &= f_{CE} = \frac{1}{2 \sin \alpha} F_B \\ f_{BD} &= f_{BE} = -\frac{1}{2 \sin \alpha} F_B \\ f_{DE} & = \frac{1}{\tan \alpha} F_B \end{aligned}$

Here, the signs are chosen so that positive forces corresonds to tensile loads and negative forces correspond to compressive loads. Since the steel girders are designed for a maximum load of 10 tons, $| f_i | \leq F_B$ must apply. This leads to the equations

$\sin \alpha \geq \frac{1}{2}, \quad \tan \alpha \geq 1 \quad \Rightarrow \quad \alpha \geq 45^\circ$

I solved the problem using a 'reciprocal diagram'. I believe this approach to frame-like structures was worked out by James Clerk Maxwell in the $19^{th}$ century. My apologies for the clunky diagrams. Maybe someone can suggest a good (free) package for drawing geometrical figures?

I assume that all the internal forces lie along the lines of the struts.

First of all label the regions of the diagram like this

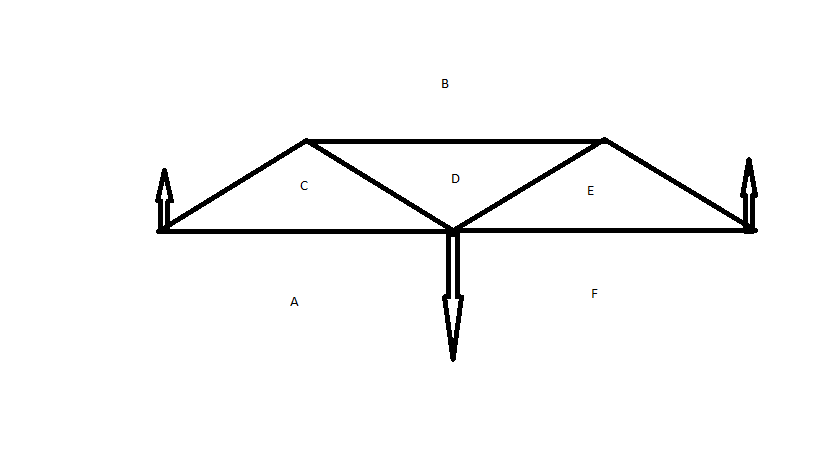
This allows us to draw the reciprocal diagram like this:-

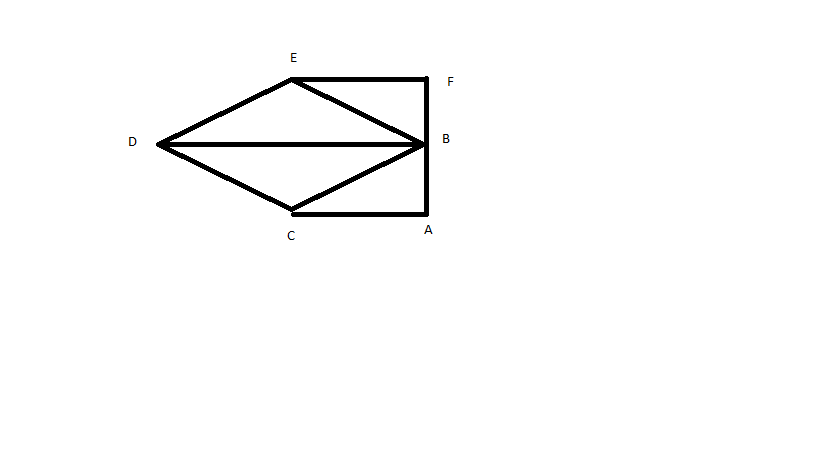
In this diagram the vertices carry the same labels as the regions in the first diagram. A line segment like EF represents the force which separates the two areas on either side of the force, in this case E and F, that is the force in the bottom right hand strut. The line segments are drawn parallel to the actual forces and their lengths are proportional to the magnitude of the forces. The diagram is constructed so that the forces acting at each point form a closed polygon, which is a necessary condition for equilibrium. You will notice that the load and the reaction forces form a triangle of zero area because the forces are parallel. With a bit of juggling (it gets easier with practice!) everything works out like a jigsaw puzzle, even although we don't yet know the actual value of $\alpha$ or the magnitudes of the internal forces.

The longest line in the diagram representing an internal force is DB (which represents the tension in the top strut). Setting the known reaction force FB to 5 and DB to 10 (its maximum permitted value), noticing that by a symmetry inherited from the first diagram E lies above the midpoint of DB, and recognising that the angle we want is EDB, it is easy to see that dropping a perpendicular from E to DB forms a right angled isosceles triangle, and so $\boxed{\alpha =45^{o}}$

Notice that if the angle is less than 45 degrees, DB becomes greater than 10 units, which is why we can say that 45 degrees is the minimum angle for an uncollapsed structure.

The ideal balance is when it is an iscoceles Triangle (with the perfect base distribution) with a 45, 45, 90 distribution