Polygon

Geometry Level 3

A convex polygon has $n$ number of sides. We cut the polygon to triangles, such that each triangle's angles are $30^\circ$ , $60^\circ$ and, $90^\circ$ . Find the maximum value of $n$ .

For example, there exists such a polygon for $n=6$ .

14 12 8 15 or more 9 13 11 10

1 solution

Áron Bán-Szabó
Jul 13, 2017

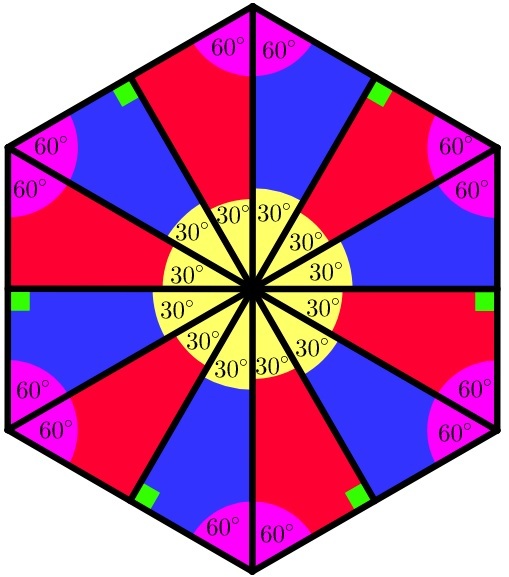
Since $30\mid 30, 60, 90$ , each of the polygon's angles is multiple of $30$ , so the maximum possible value of each angle is $150°$ . If a polygon doesn't have an angle greater than $150°$ , then the avarege of its angles isn't greater than $150°$ . So if the polygon has $k$ number of sides, the $\dfrac{(k-2)*180°}{k}\leq 150°$ By rearranging we get: $180k-360\leq 150k\Longleftrightarrow 30k\leq 360\Longleftrightarrow k\leq 12$ For $k=12$ , there exist a polygon: Therefore the answer is $\boxed{12}$ .

An excellent solution.... Beautiful and extraordinary piece of mathematics......

Utkarsh Kumar - 3 years, 11 months ago

Thank you!

Áron Bán-Szabó - 3 years, 11 months ago

Polygon

1 solution

0 pending reports