Polygon Problem 2
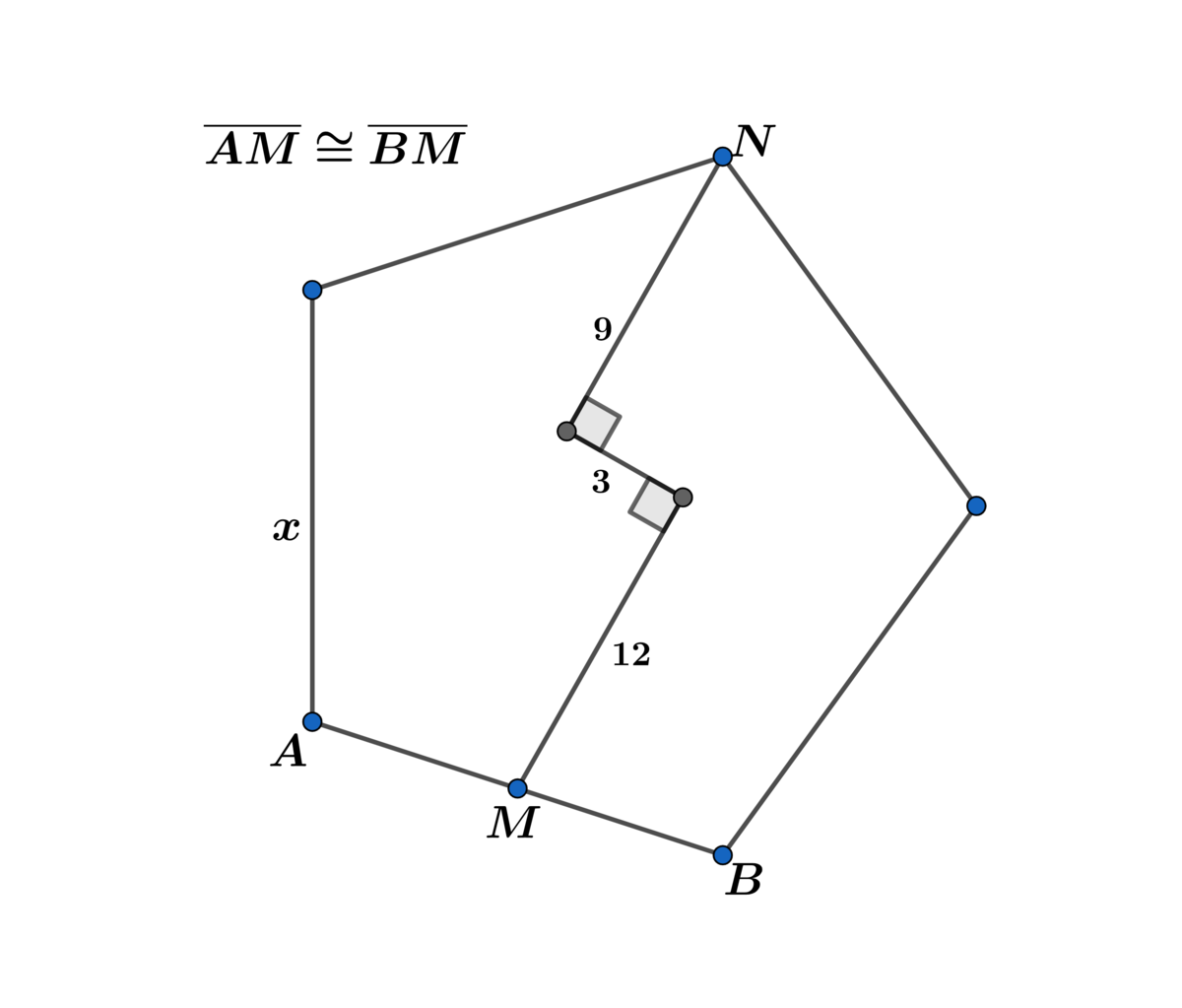
The above diagram represents a regular , where is an odd integer and and is the length of a side of the .
(1) Using the above diagram find the area of the .
(2) Using , find the area to six decimal places
The answer is 353.372164.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let n be odd integer and n ≥ 5 .
Using the diagram directly above we have:
x = 2 r sin ( n π ) and the height h = r cos ( n π ) ⟹
The area A n = 2 n sin ( n 2 π ) r 2
∣ M N ∣ = r + h = r ( 1 + cos ( n π ) = 2 r cos 2 ( 2 n π )
Using right △ M N P in the first diagram above we have:
∣ M N ∣ 2 = ( 2 r cos 2 ( 2 n π ) ) 2 = 2 1 2 + 3 2 = 4 5 0 ⟹ r = 2 1 5 2 sec 2 ( 2 n π ) = 2 1 5 sec 2 ( 2 n π )
Let r n = 2 1 5 sec 2 ( 2 n π ) ⟹
A n = 2 n sin ( n 2 π ) r n 2 = 2 n sin ( n 2 π ) ( 2 2 2 5 ) sec 4 ( 2 n π )
Using n = 1 0 1 ⟹ A 1 0 1 = 4 2 2 7 2 5 sin ( 1 0 1 2 π ) sec 4 ( 2 0 2 π )
≈ 3 5 3 . 3 7 2 1 6 4 .
Note:
Using r n = 2 1 5 sec 2 ( 2 n π ) ⟹ lim n → ∞ r n 2 = 2 2 2 5
and using the inequality cos ( x ) < x sin ( x ) < 1 we have:
π cos ( n 2 π ) < 2 n sin ( n 2 π ) < π and π lim n → ∞ cos ( n 2 π ) = π
∴ by squeeze play theorem ⟹ lim n → ∞ 2 n sin ( n 2 π ) = π
⟹
A c = lim n → ∞ 2 n sin ( n 2 π ) r n 2 = lim n → ∞ 2 n sin ( n 2 π ) ∗ lim n → ∞ r n 2 = 2 2 2 5 π ≈ 3 5 3 . 4 2 9 1 7 3 5 .