Polygon Puzzle
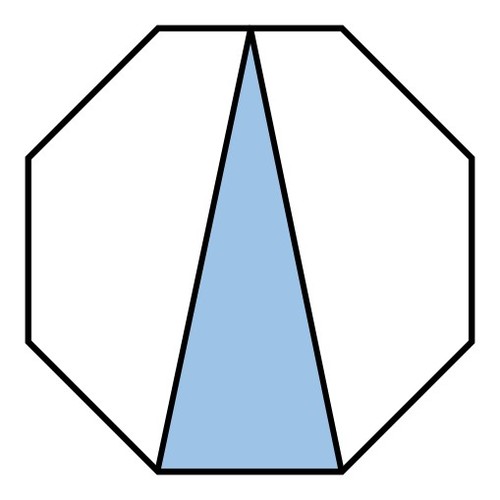 What fraction of the octagon shown is shaded?
What fraction of the octagon shown is shaded?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How do u prove that CDB is the half of CAB?
Log in to reply
CAB has the same base as CDB but double the height (because D is the octagon midpoint). Since the area of a triangle is 0 . 5 × b a s e × h e i g h t , CAB has double the area of CDB.
Nicely observed :)
The way I actually noticed is area of trapezium = 2 1 2 1 ( 2 + 2 ) = 2 1 1 ( 1 + 2 ) = area of right angled triangle, when angle at the top is shifted horizontally to left of one of the corner of the octagon.
Since line joining two opposite corner is exactly half of the octagon, equal area of trapezium and right angled triangle mean another half being the fraction of the shaded right angled triangle.
Therefore, 2 1 2 1 = 4 1 .
Answer: 4 1
Draw a vertical line from the left bottom vertex to the vertex above. Also draw a diagonal from the upper vertex to the other vertex on the bottom. This is a right triangle with 135/2 = 67.5 degree angle on the lower right. Using tan function, and considering the base (side of octagon) as 1, the vertical distance is 2.414. It can be split into three parts: 0.707, 1, 0.707. The octagon can now be split (from top to bottom) into: trapezoid, rectangle, trapezoid. The area of the rectangle is 1 * 2.414 = 2.414. The area of the trapezoids is .5 * (1 + 2.414) * 0.707 = 1.2068. The total area then is 4.8277. The area of the given triangle is .5 1 2.414 = 1.207. 1.207/4.8244 = 0.25 = 1/4.
Consider the diagram below, where point D is the centre of the octagon.
The area of triangle B C D is clearly equivalent to 8 1 of the total octagon. Meanwhile, triangle A B C has the same base but double the height of triangle B C D . The area of a triangle is given by 0 . 5 × b a s e × h e i g h t , so the area of triangle A B C is double that of triangle B C D : that is, 2 × 8 1 = 4 1 . So the answer is 4 1 .