Polygons!!
I liked a problem I saw on brillant and I altered it slightly.
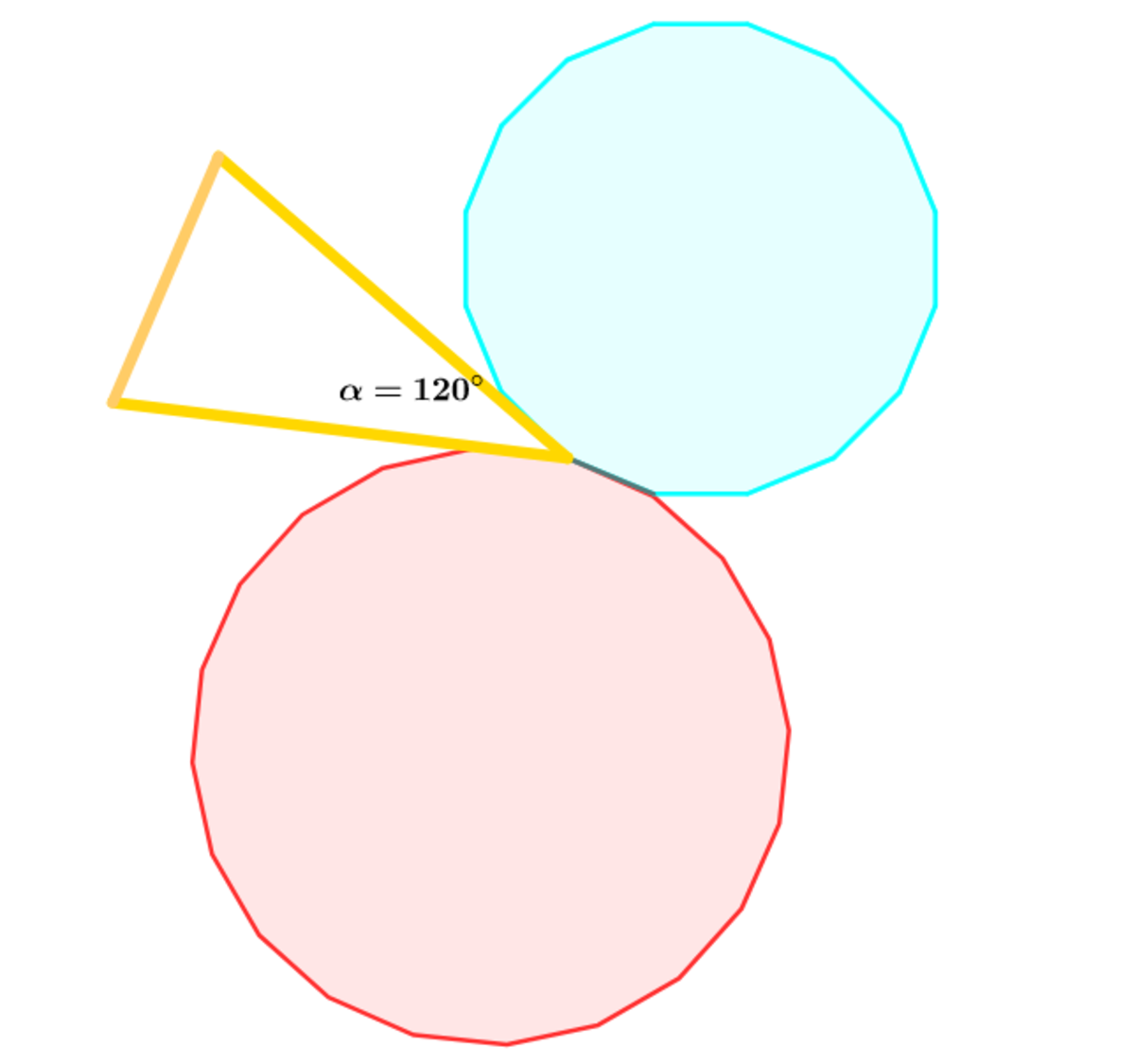
A vertex angle of an isosceles triangle and 2 other regular polygons share a single vertex in such a way that the three shapes completely cover the of space surrounding the vertex without overlapping.
(1): What is the largest possible number of sides that one of the regular polygons can have?
(2): If the area of the polygon with the larger number of sides is and the other polygon has area and is a side of the polygon with area and is a side of the polygon with area and , where and are coprime positive integers, Find .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 2 0 + ( n n − 2 ) 1 8 0 + ( m m − 2 ) 1 8 0 = 3 6 0 ⟹ n n − 2 + m m − 2 = 3 4 ⟹ m n m + n = 3 1 ⟹ m ( n ) = n − 3 3 n , where n > 3 . Since m ( n ) is monotonic decreasing for n > 3 ⟹ n = 4 maximizes m ( n ) and m ( 4 ) = 1 2 . That is; m ( n ) ≤ m ( 4 ) = 1 2 for n > 3 .
For area A of the dodecagon: Let x be a side of dodecagon.
2 x = r sin ( 1 2 π ) ⟹ r = 2 sin ( 1 2 π ) x ⟹ h = 2 x cot ( 1 2 π ) ⟹ A = 3 cot ( 1 2 π ) x 2 .
cos ( 1 2 π ) = cos ( 4 π − 6 π ) = 2 2 1 ( 3 + 1 )
sin ( 1 2 π ) = sin ( 4 π − 6 π ) = 2 2 1 ( 3 − 1 )
⟹ A = 3 ( 3 − 1 3 + 1 ) x 2 = 3 ( 2 + 3 ) x 2
A = 3 ( 2 + 3 ) x 2 = 2 + 3 ⟹ x = 3 1 .
The area of the square A ∗ = y 2 = 2 ⟹ y = 2
⟹ x y = 3 2 = b a ⟹ a + b = 5 .