Polygons and a circle
Given any polygon with perimeter 1, can a circle with radius
4
1
always enclose the polygon?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Nice constructive proof! It's easy to show that 1/4 is a sharp lower bound too for radius of the covering circle. We could use an isosceles triangle with base diminishing to zero, then each leg approaches 1/2, thus the diameter of covering circle has to be at least 1/2.
This sounds like a fascinating proof but I am stuck understanding the penultimate step.
Could you please explain why A K B M being a parallelogram implies A M + M B ≤ 2 1 ?
Log in to reply
@Agnishom Chattopadhyay - The statement is true because the broken line is longer than the length of the link connecting the two endpoints, not because the AKBM is a parallelogram.
Log in to reply
By "broken line" you mean "perimeter of the figure" and "two endpoints" you mean "A and M" and "M and B" respectively. Basically the shortest path from A to M is the segment AM and the shortest path from M to B is the segment AB. Thus AM + AB <= the semi-perimeter value of 1/2.
Okay, that makes perfect sense. Thanks!
Suppose we have any polygon inside the circle. choose any two points on the perimeter of the polygon and draw a line between them. Let's assume that the line's length is more than 0.5 (for example 0.5001) in this case the polygon wouldn't be enclosed completely inside the circle because the circle has a diameter of 0.5. Now choose any of the two points. Because a polygon is a closed shape, we know that there must be two different paths between the two points and the sum of the lengths of these two paths is the perimeter of the polygon. We know that the shortest distance between two points is a straight line (which in this case is 0.5001), therefore, the length of any of the two paths must be greater than/or equal to 0.5001 which means that the perimeter must be greater than 1.
Great simple answer
A small addition to your solution. A triangle is also considered a polygon, and for a triangle, your proof doesn't work. The triangle case can be proven similarly, by showing that if a side must be > 0.5 (so that is not enclosed by the circle), and in order for the triangle the sum of the other 2 sides must be > then 0.5. So again the sum will be bigger than 1 (the allowed perimeter).
It is known that increasing the sides of a polygon by keeping the perimeter fixed will increase the area of the polygon. Starting from a triangle, a square... the cicrle is the maximum we can go to (with infinite number of point sides.) If by keeping the perimeter fixed at 1 the circle resulting will have an area bigger than the area of preceding polygons, then the given circle of perimeter P=2 pi/4 = 2× 3.14/4= 1.57 > 1, will definitely have a bigger area than the circle of perimeter 1, which already encompasses the polygon of perimeter 1, hence the given circle will encompass the polygon de facto.
That shows that the circle must have a bigger area than the polygon, not that it must enclose it. A circle of perimeter 1 (and hence diameter 1/pi = ~0.3) doesn't enclose every polygon of perimeter 1 - consider a long thin rectangle with sides (0.5-epsilon) and epsilon.
Circle radius = 4 1 = .25 <space> Circle diameter = 2 1 = .50 Circle Circumference =2 π r = 2 π .25 = 1.57
Polygon (triangle) = perimeter 1 Side A = 0.3 Side B = 0.3 Side C = 0.4
Because the polygon has a perimeter of 1 (divided between at least 3 sides) it will always fit with in a circumference with a radius of at least .25 or 4 1
This is wrong. You didn't properly answer this question. The question asks for
Given any polygon with perimeter 1...
But what you did was
Let's start with a scalene triangle with perimeter 1...
We can also rewrite the question as what would be the longest side of a polygon whose perimeter is 1. The lesser number the sides, the longer can the sides be with a fixed perimeter value. Hence we check for a triangle.
Triangle longest side should be <= 0.5 for the circle to enclose it.
Let's take a triangle with the side 0.5 . The other two sides would both be 0.25. They would meet the 0.5 side in the middle creating a line rather than a triangle. The only way a triangle of perimeter 1 would work is if it's longest side is less than 0.5. we have already proved that this can be the longest side of any polygon with perimeter 1. Hence the circle can enclose it.
Consider how you would go about making a polygon as wide as possible for a perimeter of 1. The simplest approach is to take a rectangle and make it as wide as possible i.e. with width close to 1/2 and height close to 0. Clearly this can still be enclosed by the circle radius 1/4.
If the longest line you can draw is 1/2, then you cannot return to your starting point w/o drawing 2 lines with a sum greater than 1/2.
The semantics of "given any polygon" and "does there exist a polygon" is irrelevant when considering the trivial case:
Two parallel lines with length 1/2, perimeter 1, will still be enclosed in the circle of diameter 1/2. Any shape with 2 or more sides will therefore have a smaller effective diameter than 1/2. So if any shape with more than 1 side is enclosed in the circle, isn't the general case for "any polygon" pointless?
I believe this is what Scott Rodham was claiming.
No, there's a difference between "I can use any polygon" versus "I got a specific polygon".
Even a trivial polygon "along" a diameter of 1/2 is contained.
Note that the problem says "for any polygon". It does not ask "does there exist a polygon". There is a huge difference between these 2 conditionals.
As Scott Rodham says - consider the trivial polygon of a line length = 1/2, therefore it's "perimeter" is 1. The trivial polygon has a total length of 1/2 which can fir in the circle of radius 1/4 or diameter 1/2.
one has to assume that the diameter of the polygon (if modelled as a circle) is to be 1/pi so the polygon is enclosed
It's only a particular configuration, you have to show it for every possible one! (Considering the "worst" possible case isn't sufficient)
To make this polygon as long and flat as possible, we want to give it the fewest number of sides. So, we make it a triangle. Since the perimeter is 1, we know that the sum of the three side lengths is 1, but we also know that the sum of the two shortest sides has to be greater than the third side. Those two conditions imply that the longest side length of this triangle has to be strictly less than 1/2. Since the diameter of this circle equals 1/2, it is impossible to construct a polygon that cannot be contained by this circle.
Are you assuming that the polygon is regular? We could have made it a really long rectangle, or even a "dumbbell shape".
In fact, I'd go as far as to say any arbitrary polygon of fixed perimeter can be fitted into an infinitesimal circle. An arbitrary convex polygon of unit perimeter can off course fit into a circle radius > 1/(2π).
While the conclusion is correct, it doesn't automatically follow from the argument. While the longest side of the triangle must be less than 1/2, the circle only equals 1/2 on a diameter. If the polygon is displaced slightly, the length of a chord parallel to the side of the triangle is less than 1/2 also. In the case of the triangle, it must be shown that the third corner does not cross the perimeter of the circle when the long side is on a diameter. For example, if the two shortest sides are not comparable in size, we could have an isosceles triangle with two long sides and a narrow base. If we put one of the long sides on a diameter, can we guarantee that the third corner will not stick out? If we orient the triangle so that the small angle is bisected, then the circle does contain it, but that is not how your argument reads.
To make the polygon as long and flat as possible, I would pick a rectangle. Seems flatter than a triangle.
We will prove that if a polygon's perimeter is 1 then we can cover it with a circle which has a radius of 4 1 .
Let A be a random point at the perimeter of the polygon. Imagine we are walking around the polygon's perimeter form A , and we walk exactly 2 1 then we stop. Let B the poin where we stopped. Furthermore, let O be the midpoint of A B . Write a circle which has a radius of 4 1 around O . If M is another point (not A and B ) at the perimeter of the polygon, and K is the M ′ s mirror image of O , then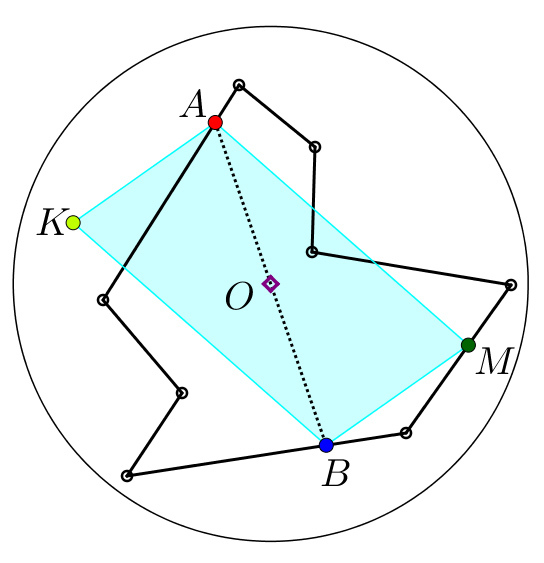
M K = 2 O M ≤ A M + A K = A M + M B ≤ 2 1 O M ≤ 4 1 (because A K B M is a paralelogram).
So the circle completely covers the polygon.