Polygons in squares!
A
th squared figure is defined as a set of concentric squares in a plane such that the diagnols of the largest square is crossed.
For example the first squared figure is
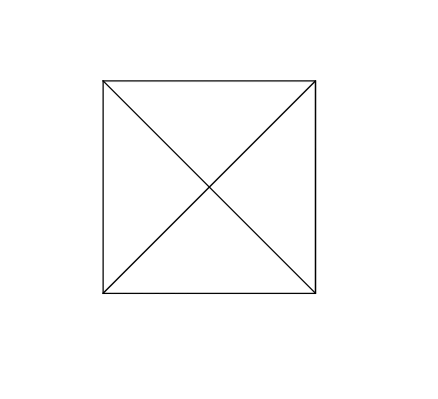
The second squared figure is

The third squared figure is
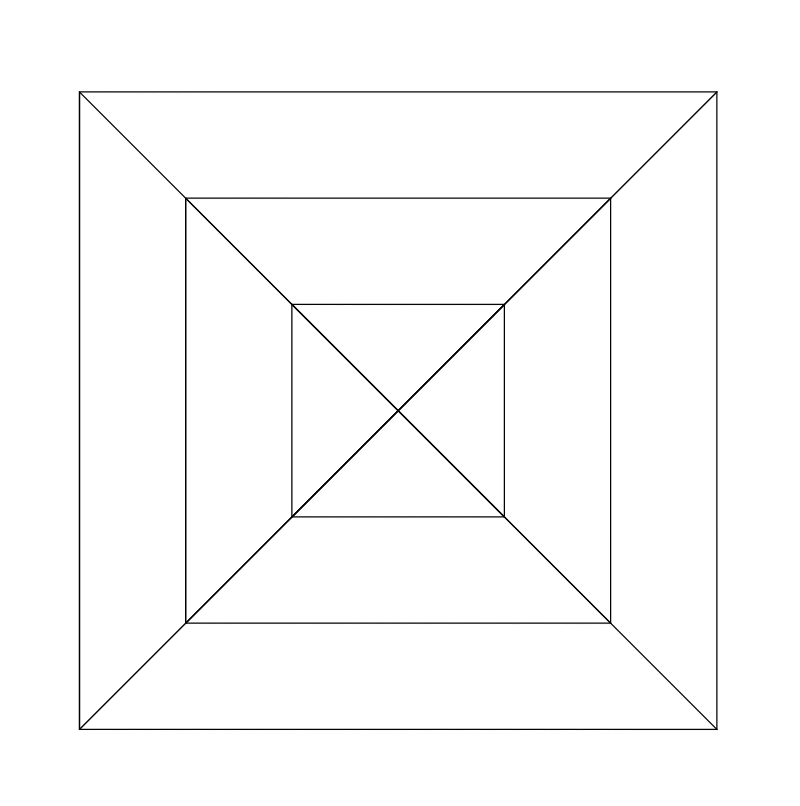
Let denote the number of triangles, denote the number of quadrilaterals, denote the number of pentagons and denote the number of hexagons in the th squared figure, Compute . The answer is of the form , where and are coprime positive integers. Submit the value of .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us work on the 5th figure and logically generalize for the n t h squared figure.
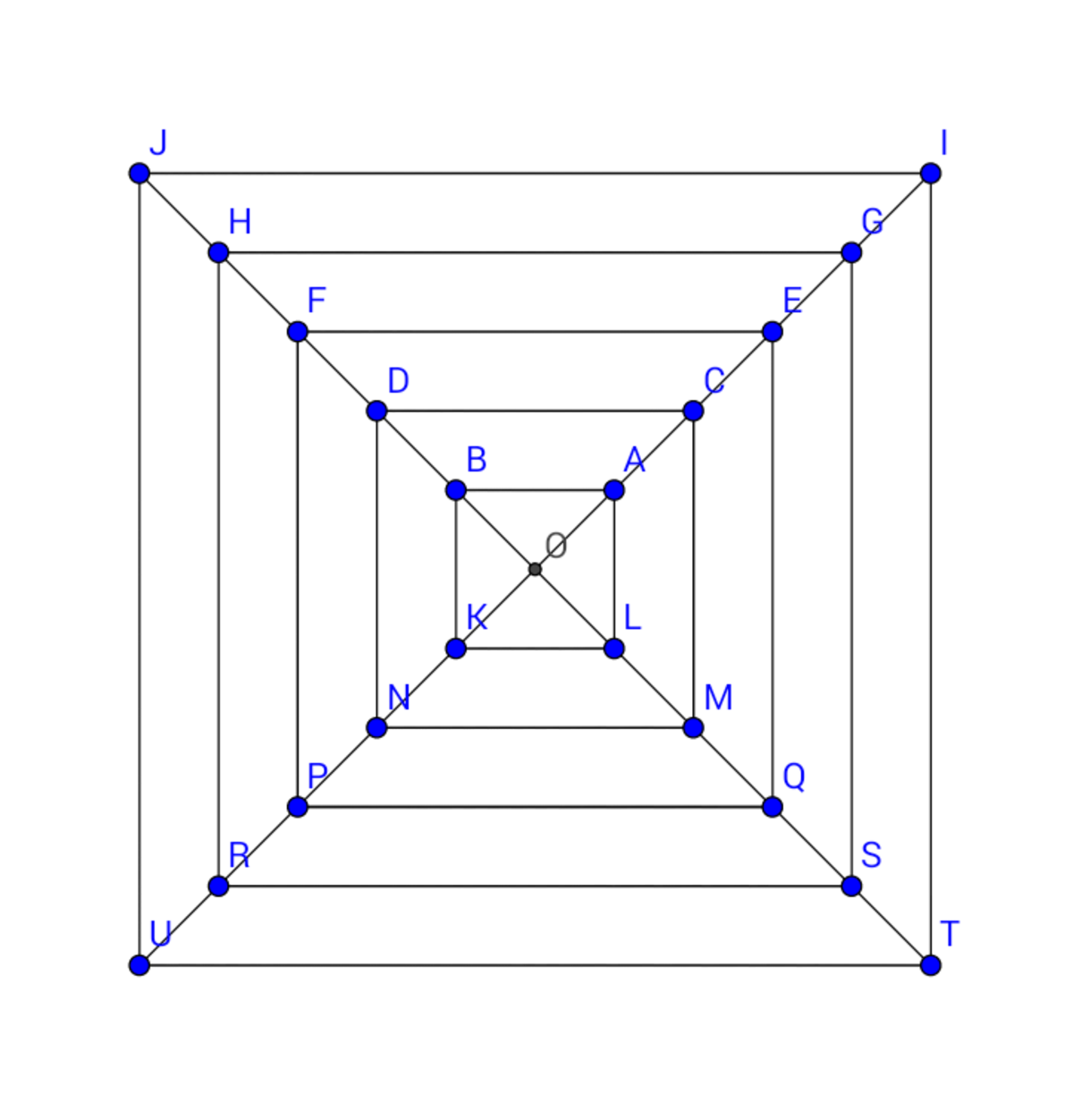
Consider the figure to be divided into four sections. The first section is △ J O I . The second section is △ J O U , the third section is △ U O T and the fourth section is △ T O I .
To find the number of triangles in this figure is quite simple.
One triangle embedded in the figure is △ O A B .
To find the number of such triangles, consider the point O as one vertex of the triangle. Now, the third side can be either one of A B , D C , E F , G H or I J . So, it makes 5 of them. There are similar triangles in the four sections, which makes 5 × 4 = 2 0 of them.
Logically thinking, if we had the n t h squared figure we would have 4 n of them. ⟶ 1 .
Another type of triangles is of the type △ A B K . Observe that if the vertex B is changed to D then we get △ D N C . Similarly, change the vertices to F , H and J to get three more of such triangles. This makes 5 of them. Here we have consider the sections 1 and 2, there are five such triangles each in section(2 and 3), section(3 and 4), section(4 and 1). This makes 5 × 4 = 2 0 of them.
Logically thinking, if we had the n t h squared figure we would have 4 n of them. ⟶ 2 .
From 1 and 2 we would get 4 n + 4 n = 8 n triangles in the n t h squared figure.
To find the number of quadrilaterals.
One type is □ A B C D . Fix A B as one side of the trapezium. The opposite side can be C D , E F , H G or J I . This makes 4 of them. Now if we take the base as C D and start selecting the opposite side, observe that we have already counted the one is which we would be taking A B as the opposite side, so the choices for the opposite side to be selected decreases to three. Then for base E F we have two choices for the opposite side and for base G H only one. So the number of such quadrilaterals are 4 + 3 + 2 + 1 = 1 0 . Now, there would be similar trapezium in all the four sections making it 1 0 × 4 = 4 0 of them.
Logically thinking, if we had the n t h square figure we would have 4 [ ( n − 1 ) + ( n − 2 ) + ⋯ + 2 + 1 ] = 2 n ( n − 1 ) of them. ⟶ 3 .
Another type of quadrilaterals embedded here are the concentric squares visible . Here there are 5 of them. Obviously, the n t h square figure would have n of them. ⟶ 4
Another type of quadrilaterals is of the form J B K I . Here we consider one base line in section one and one perpendicular line in section 2. Suppose we consider J I as the base line then we can form such quadrilaterals by choosing the base line as H R , F P , D N or B K . Now, if we change the base line to line G H , we would have only 3 options for the perpendicular line. If the base line was E F , then the options would decrease to two and for base line C D only C D B K is possible. This makes 4 + 3 + 2 + 1 = 1 0 of them. But we can also consider the base line to be in section 2 and the perpendicular line to be in section 1. This makes 1 0 + 1 0 = 2 0 in each two consecutive sections. Now there are our such consecutive sections, this makes 2 0 × 4 = 8 0 such quadrilaterals. Logically thinking, if we had the n t h square figure we would have 2 ( 4 [ ( n − 1 ) + ( n − 2 ) + ⋯ + 2 + 1 ] ) = 4 ( n − 1 ) n of them. ⟶ 5 .
From 3 , 4 and 5 , we get the total number of quadrilaterals in the n t h squared figure as 2 n ( n − 1 ) + n + 4 ( n − 1 ) n = n ( 6 n − 5 ) of them.
Now, to find the number of pentagons is quite simple.
There is only one type of pentagons in this figure. A B O K L is one of them, here the base line is A L , there are four more such pentagons which can be obtained by changing the base line to C M , E Q , G S or I T . This makes 5 of them. Now, there are four such sections, making a total of 5 × 4 = 2 0 of them.
Logically thinking, if we had the n t h squared figure we would have 4 n of them.
Now, to find the number of hexagons.
One type of hexagons is D B A L M C . Here the “opposite vertices” are A and C . So, the number of hexagons in this section can be obtained by finding the total number of pairs of opposite vertices which can be selected from the lot of A , C , F , G and I . This can be given by ( 2 5 ) = 1 0 . Now there are four such consecutive sections, so a total of 1 0 × 4 = 4 0 such hexagons can be obtained. Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 n ) = 2 n ( n − 1 ) of them. ⟶ 6 .
Another type of hexagons is J H R U T I . Here, J and H can be considered as the “edge points” of this hexagon. Now, the number of such hexagons can be obtained by choosing a pair of the possible edge points J , H , F , D , B which can be given by ( 2 5 ) . Now there are four such sections possible so the number of such hexagons is 4 × ( 2 5 ) = 4 0 . . Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 n ) = 2 n ( n − 1 ) of them. ⟶ 7 .
Another type of hexagons is J H R S T I . Here, J and H can be considered as the “edge points” of this hexagon. Now, the number of such hexagons can be obtained by choosing a pair of the possible edge points J , H , F , D , B which can be given by ( 2 5 ) . Now there are four such sections possible so the number of such hexagons is 4 × ( 2 5 ) = 4 0 . . Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 n ) = 2 n ( n − 1 ) of them. ⟶ 8 .
Another type of hexagons is J H R S G I . Here, J and H can be considered as the “edge points” of this hexagon. Now, the number of such hexagons can be obtained by choosing a pair of the possible edge points J , H , F , D , B which can be given by ( 2 5 ) . Now there are four such sections possible so the number of such hexagons is 4 × ( 2 5 ) = 4 0 . . Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 n ) = 2 n ( n − 1 ) of them. ⟶ 9 .
Another type of hexagons is J H R O T I . Here, J and H can be considered as the “edge points” of this hexagon. Now, the number of such quadrilaterals can be obtained by choosing a pair of the possible edge points J , H , F , D , B which can be given by ( 2 5 ) . Also, this hexagon is not symmetrical as the previous hexagons. So, for the two consecutive sections, the number of such hexagons is 2 ( 2 5 ) = 2 0 . Now there are four such sections possible so the number of such hexagons is 4 × 2 0 = 8 0 .. Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 × ( 2 n ) ) = 4 n ( n − 1 ) of them. ⟶ 1 0 .
Another type of hexagons is J H R S O I . Here, J and H can be considered as the “edge points” of this hexagon. Now, the number of such quadrilaterals can be obtained by choosing a pair of the possible edge points J , H , F , D , B which can be given by ( 2 5 ) . Also, this hexagon is not symmetrical as the previous hexagons. So, for the two consecutive sections, the number of such hexagons is 2 ( 2 5 ) = 2 0 . Now there are four such sections possible so the number of such hexagons is 4 × 2 0 = 8 0 .. Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 × ( 2 n ) ) = 4 n ( n − 1 ) of them. ⟶ 1 1 .
Another type of hexagons is J O G S T I , the number of such hexagons is 4 × 2 0 = 8 0 .. Logically thinking, if we had the n t h squared figure we would have 4 × ( 2 × ( 2 n ) ) = 4 n ( n − 1 ) of them. ⟶ 1 2 .
So, from 6 , 7 , 8 , 9 , 1 0 , 1 1 , 1 2 the total number of hexagons in the figure is 2 0 n ( n − 1 ) .
Therefore, δ n = 8 n , β n = n ( 6 n − 5 ) , γ n = 4 n , δ n = 2 0 n ( n − 1 ) .
n → ∞ lim α n × β n δ n × γ n ∴ a + b = 5 + 3 = 8 n × n ( 6 n − 5 ) 2 0 n ( n − 1 ) × 4 n = 4 8 8 0 = 3 5 = 8