Square root is a one to one mapping

Algebra Level 5

C o n j u g a t e ( x ) = 1 + 1 − x Conjugate (x) = \sqrt {1 + \sqrt{1 - x}}

Which of the following is an answer to the above equation?

In the options, j = − 1 j = \sqrt{-1 } .

1.6180339887498948482045868343656 1.6180339887498948482045868343656 0.22298594482978 + j 0.41336379625112 1.12114689645950 + j 0.18434863333096 0.6180339887498948482045868343656 0.6180339887498948482045868343656 0 − 0.6180339887498948482045868343656 -0.6180339887498948482045868343656

View wiki
Lu Chee Ket by Lu Chee Ket , 47, Malaysia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Lu Chee Ket
Feb 24, 2015

1 Helpful 0 Interesting 0 Brilliant 0 Confused

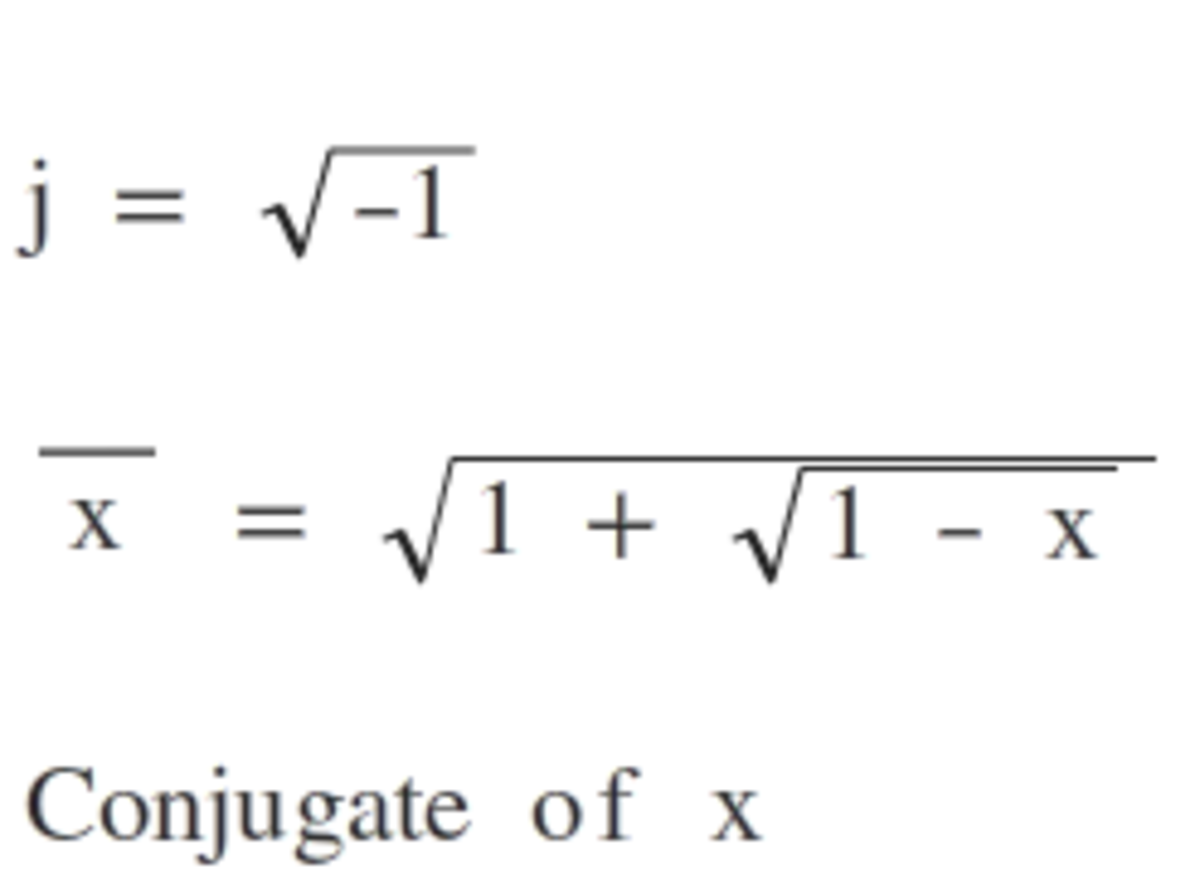
Can you explain how you arrived at your answer?

Even if we square both sides repeatedly, we arrive at

( x 2 − 1 ) 2 = 1 − x ( x^2 -1 ) ^ 2 = 1 -x

which is equal to ( x ( x − 1 ) ( x 2 + x − 1 ) = 0 (x ( x-1) ( x^2 + x - 1 ) = 0 . The roots are thus x = 0 , 1 , 1 2 ( − 1 ± 5 ) x = 0, 1, \frac{1}{2} ( -1 \pm \sqrt{5} ) .

Note that we will still have to verify that these are indeed valid solutions, which they might not be. (e.g. x=0 is not a solution)

Calvin Lin Staff - 6 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...