Polynomial of Root

Algebra Level 3

28 + 10 3 + 28 − 10 3 + 6 + 4 2 + 6 − 4 2 = ? \sqrt{28+10\sqrt3} + \sqrt{28 - 10\sqrt3} + \sqrt{6 + 4\sqrt2} + \sqrt{6-4\sqrt 2} = \ ?


The answer is 14.

View wiki
Dhira Tengara by Dhira Tengara , 19, Indonesia

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

3 solutions

Let 28 + 10 3 + 28 − 10 3 = x \sqrt{28+10\sqrt{3}} + \sqrt{28-10\sqrt{3}}\ = x and 6 + 4 2 + 6 − 4 2 = y \sqrt{6+4\sqrt{2}} + \sqrt{6-4\sqrt{2}}\ = y

x 2 = 28 + 10 3 + 2 2 8 2 − 1 0 2 ( 3 ) + 28 − 10 3 x 2 = 56 + 2 484 x 2 = 56 + 2 ( 22 ) x 2 = 100 x = 10 x^2 = 28+10\sqrt{3} + 2\sqrt{28^2-10^2(3)} + 28 - 10\sqrt{3} \\x^2 = 56 + 2\sqrt{484} \\x^2 = 56 +2(22) \\x^2 = 100 \\\boxed{x= 10}

y 2 = 6 + 4 2 + 2 6 2 − 4 2 ( 2 ) + 6 − 4 2 y 2 = 12 + 2 4 y 2 = 12 + 2 ( 2 ) y 2 = 16 y = 4 y^2 = 6+4\sqrt{2} + 2\sqrt{6^2-4^2(2)} + 6 - 4\sqrt{2} \\y^2 = 12 + 2\sqrt{4} \\ y^2 = 12 +2(2) \\y^2 = 16 \\\boxed{y = 4}

x + y = 10 + 4 = 14 x+y = 10+4 = \large{\boxed{14}}

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Like Dhira Tengara's solution, you didn't show that all the expressions inside their respective radicals are non-negative. It is important because the answer would turn out wrong if we were to solve − 1 + − 4 + − 9 + − 16 \sqrt{-1} + \sqrt{-4} + \sqrt{-9} + \sqrt{-16} .

It's obvious that 28 + 10 3 > 0 28 + 10\sqrt3 > 0 because it is the sum of two positive terms, but it is not obvious that 28 − 10 3 > 0 28 - 10\sqrt3 > 0 . Consider the square of 28 28 and 10 3 10\sqrt3 which are 784 784 and 300 300 respectively. Thus ( 28 + 10 3 ) ( 28 − 10 3 ) = 784 − 300 > 0 ( \sqrt{28} + 10\sqrt3)(\sqrt{28} - 10\sqrt3) = 784 - 300 > 0 then either 28 + 10 3 , 28 − 10 3 28 + 10\sqrt3, 28 - 10\sqrt3 are both negative or both positive. Since we have shown that one of them is positive, the other must be positive as well.

Can you prove that 6 − 4 2 > 0 6 - 4\sqrt2 > 0 from here?

Sorry about that.

To prove that 6 − 4 2 6-4\sqrt{2} is positive we take the square of 6 6 and square of 4 2 4\sqrt{2} which give 36 36 and 32 32 respectively. By performing difference of two squares we get that 36 − 32 = 4 36-32 = 4 , which is a positive number. From a 2 − b 2 = ( a + b ) ( a − b ) a^2 - b^2 = (a+b)(a-b) its factors are ( 6 + 4 2 ) (6 + 4\sqrt{2}) and ( 6 − 4 2 ) (6 - 4\sqrt{2}) and to get a positive product, you need the two factors to be both positive or both negative. Since 6 + 4 2 6 + 4\sqrt{2} is positive, 6 − 4 2 6 - 4\sqrt{2} is positive also.

Justine Allen Arciga - 6 years ago

Log in to reply

Another way to prove that it's nonnegative.

10 3 = 300 10 \sqrt{3} = \sqrt{300}

324 > 300 \sqrt {324} > \sqrt{300}

18 > 300 18 > \sqrt {300}

28 > 18 > 300 28 > 18 > \sqrt {300}

So 28 − 10 3 28 - 10 \sqrt{3} is positive.

Likewise, 4 2 = 32 4 \sqrt{2} = \sqrt{32}

36 > 32 \sqrt {36} > \sqrt {32}

6 > 32 6 > \sqrt {32}

So 6 − 4 2 6 - 4\sqrt{2} is positive also.

Justine Allen Arciga - 6 years ago
Dhira Tengara
Jun 1, 2015

All the expressions inside the radicals are all non-negative.

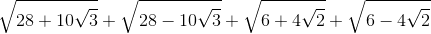
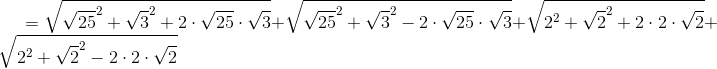
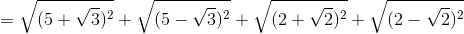
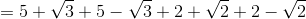
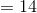
1 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Almost correct. You need to make sure that all the expressions inside the radicals are all non-negative, else you would be dealing with complex numbers. And it would be better to clarify how you move from step 1 to step 2 of your solution.

Ins response to Dhira Tengara: Just make sure you have written out all the details :

28 + 10 3 = 25 2 + 3 2 + 2 ⋅ 25 ⋅ 3 \sqrt{28 + 10\sqrt{3}} = \sqrt{\sqrt{25}^{2} + \sqrt{3}^{2} + 2\cdot \sqrt{25}\cdot \sqrt{3}}

In response to the Challenge Master:

Wow! There are a lot of Challenge Master notes these days . Superb!

A Former Brilliant Member - 6 years ago
Vadlamani Madhav
Jun 16, 2015

By taking square root of that polynomial we get 5+5+2+2=14 and other terms get cancelled.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...