Polynomial powered by 2
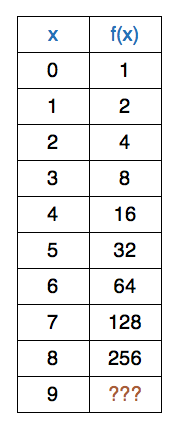 A polynomial
f
(
x
)
has degree
8
and
f
(
i
)
=
2
i
for
i
=
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
.
A polynomial
f
(
x
)
has degree
8
and
f
(
i
)
=
2
i
for
i
=
0
,
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
.
Find f ( 9 ) .
The answer is 511.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
I was doing the same way, but mid-way, I saw the pattern that the difference between succesive diagonals was just 1.
The reason the last row must be constant is that the polynomial has 8-degree, right?
wow my answer is 512 because it is only multiplying by 2
Solution 1: Since we have 9 values for a degree 8 polynomial, this polynomial is uniquely determined.
For i a non-negative integer, consider the polynomial ( i x ) = i ! ( x ) ( x − 1 ) ⋯ ( x − i + 1 ) . It is clear that f ( n ) = ∑ i = 0 8 ( i n ) for n = 0 to 8. Hence, this must be the unique polynomial.
Thus, f ( 9 ) = ∑ i = 0 8 ( i 9 ) = ( 1 + 1 ) 9 − ( 9 9 ) = 5 1 1 .
Solution 2: By the Lagrange Interpolation Formula, f ( 9 ) = i = 0 ∑ 8 ( j = 0 ∏ i − 1 ( i − j ) ) ⋅ ( j = i + 1 ∏ 8 ( i − j ) ) 2 i ⋅ ( j = 0 ∏ i − 1 ( 9 − j ) ) ⋅ ( j = i + 1 ∏ 8 ( 9 − j ) ) This equals i = 0 ∑ 8 i ! ⋅ ( − 1 ) 8 − i ( 8 − i ) ! 2 i ⋅ 9 ! / ( 9 − i ) = i = 0 ∑ 8 2 i ⋅ ( − 1 ) 8 − i i ! ( 9 − i ) ! 9 ! = − i = 0 ∑ 8 2 i ( − 1 ) 9 − i i ! ( 9 − i ) ! 9 ! By the Binomial Theorem applied to ( 2 − 1 ) 9 , this equals − ( ( 2 − 1 ) 9 − 2 9 ) = 2 9 − 1 = 5 1 1
Solution 3: Since we know that f ( x ) is a polynomial, we use the method of finite differences. We construct the table of differences as follows:
1 1 2 1 2 1 4 2 1 4 2 1 8 4 2 1 8 4 2 1 1 6 8 4 2 1 1 6 8 4 2 3 2 1 6 8 4 h 3 2 1 6 8 g 6 4 3 2 1 6 f 6 4 3 2 e 1 2 8 6 4 d 1 2 8 c 2 5 6 b a f ( 9 )
This allows us to calculate that h = 1 , g = 3 , f = 7 , e = 1 5 , d = 3 1 , c = 6 3 , b = 1 2 7 , a = 2 5 5 , f ( 9 ) = 5 1 1 .
how to do it using Polynomial Interpolation?
Great problem. More thanks for attaching the method of differences wiki.
We have to find an 8 degree polynomial, namely f ( x ) , so that we can find the value of f ( 9 ) , since i = 9 . Let us consider 9 polynomial functions P 0 ( x ) , P 1 x ) , P 2 ( x ) . . . P 8 ( x ) .
Now
Let P ( x ) = ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 6 ) ( x − 7 ) ( x − 8 ) Then P ( 0 ) = ( − 1 ) ( − 2 ) ( − 3 ) ( − 4 ) ( − 5 ) ( − 6 ) ( − 7 ) ( − 8 ) ⇒ P ( 0 ) = 8 ! so, P 0 ( x ) = 8 ! 1 ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) … ( x − 8 )
let P ( x ) = x ( x − 2 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 6 ) ( x − 7 ) ( x − 8 ) Then, P ( 1 ) = ( 1 ) ( − 1 ) ( − 2 ) ( − 3 ) ( − 4 ) ( − 5 ) ( − 6 ) ( − 7 ) ⇒ P ( 1 ) = − ( 7 ! ) so, P 1 ( x ) = 7 ! − 1 x ( x − 2 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 6 ) ( x − 7 ) ( x − 8 )
Let P ( x ) = x ( x − 1 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 6 ) ( x − 7 ) ( x − 8 ) Then, P ( 2 ) = ( 2 ) ( 1 ) ( − 1 ) ( − 2 ) ( − 3 ) ( − 4 ) ( − 5 ) ( − 6 ) ⇒ P ( 2 ) = ( 6 ! ) ( 2 ) so, P 2 ( x ) = ( 6 ! ) ( 2 ) 1 x ( x − 1 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 6 ) ( x − 7 ) ( x − 8 ) Similarly, we can get the following: P 3 ( x ) = ( 3 ! ) ( 5 ! ) − 1 x ( x − 1 ) ( x − 2 ) ( x − 4 ) ( x − 5 ) … ( x − 8 ) P 4 ( x ) = 4 ! 4 ! 1 x ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 5 ) ( x − 6 ) … ( x − 8 ) P 5 ( x ) = 5 ! 3 ! − 1 x ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) ( x − 6 ) … ( x − 8 ) P 6 ( x ) = 6 ! 2 ! 1 x ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 7 ) ( x − 8 ) P 7 ( x ) = 7 ! − 1 x ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) ( x − 5 ) ( x − 6 ) ( x − 8 ) P 8 ( x ) = 8 ! 1 x ( x − 1 ) ( x − 2 ) ( x − 3 ) ( x − 4 ) … ( x − 7 )
Now, f ( x ) = P 0 ( x ) + 2 P 1 ( x ) + 4 P 2 ( x ) + 8 P 3 ( x ) + 1 6 P 4 ( x ) + 3 2 P 5 ( x ) + 6 4 P 6 ( x ) + 1 2 8 P 7 ( x ) + 2 5 6 P 8 ( x ) Since: f ( i ) = 2 i for i = 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 See The post on Lagrange Interpolation Formula.(To understand the above usage). Substituting for x = 9 in the above equation we get the following: f ( 9 ) = 1 − 1 8 + 1 4 4 − 6 7 2 + 2 0 1 6 − 4 0 3 2 + 5 3 7 6 − 4 6 0 8 + 2 3 0 4 ⇒ f ( 9 ) = 5 1 1
This solution is truly a brute force one. Lagrange Interpolation Formula does work, of course, but it is messy and does not reveal the structure of the problem. The Newton Interpolation Method, which is essentially used in the suggested solution, works much nicer here. Nevertheless, this solution is perfectly legitimate, and pretty well written.
The much better approach is to show that the polynomial ∑ i = 0 8 ( i n ) satisfies the conditions. Hence, the answer is f ( 9 ) = ∑ i = 0 8 ( i 9 ) = ( 1 + 1 ) 9 − 1 = 5 1 1 .
We see that the sequence of values of f ( i ) for i = 0 , 1 , … , 9 are: ( 1 , 2 , 4 , 8 , 1 6 , 3 2 , 6 4 , 1 2 8 , 2 5 6 ) . Next we see the difference between adjacent values to produce first order difference: ( 1 , 2 , 4 , 8 , 1 6 , 3 2 , 6 4 , 1 2 8 ) , we repeat until we reach a constant value: ( 1 ) , which is the eighth order difference. Since f ( i ) is of order 8 , there must be only one polynomial that satisfies that eighth order difference of ( 1 ) , and it must be constant. So the second term of the eighth order difference should also be 1 . Therefore we have the seventh order of difference: ( 1 , 2 , 3 ) , the sixth ( 1 , 2 , 4 , 7 ) , the fifth ( 1 , 2 , 4 , 8 , 1 5 ) , and so on until the values ( 1 , 2 , 4 , 8 , 1 6 , 3 2 , 6 4 , 1 2 8 , 2 5 6 , 5 1 1 ) . So f ( 9 ) = 5 1 1 .
We can solve this by using Lagrange Interpolation Formula. By using the formula, the answer = 511
F(x) is a polynomial of degree 8. We know nine values of f(x), so we can use Lagrange interpolation formula; So, f(9)=1 ( (9-1) (9-2) (9-4) (9-8)...(9-256)/(0-1) (0-2) (0-4) (0-8)...(0-256)) + 2 *(((9-0) (9-2) (9-4) (9-8)...(9-256)/(1-0) (1-2) (1-4) (1-8)...(1-256))+ ...+ 256 (((9-0) (9-1) (9-2) (9-4)...(9-128)/(8-0) (8-1) (8-2) (8-3)...(8-7))=511
Since f(x) has degree 8, we assume it is of the following form:
a 1 + a 2 x + a 3 x 2 + a 4 x 3 + a 5 x 4 + a 6 x 5 + a 7 x 6 + a 8 x 7 + a 9 x 8 = f ( x )
Since f ( i ) = 2 i for i = 0, 1, 2, 3, 4, 5, 6, 7 and 8, we know that
f ( 0 ) = 1 , f ( 1 ) = 2 , f ( 2 ) = 4 , f ( 3 ) = 8 , f ( 4 ) = 1 6 , f ( 5 ) = 3 2 , f ( 6 ) = 6 4 , f ( 7 ) = 1 2 8 , f ( 8 ) = 2 5 6
We can now make 9 equations by plugging in each x value and f(x) value into the original equation.
Solving the system of 9 equations will get you the following coefficients:
a 1 = 1 a 2 = 8 4 0 5 2 3 a 3 = 2 0 1 6 7 9 9 a 4 = 2 8 8 − 3 1 a 5 = 6 4 0 6 3 a 6 = 7 2 0 − 1 9 a 7 = 1 9 2 1 a 8 = 2 0 1 6 − 1 a 9 = 4 0 3 2 0 1
Plugging in x = 9 to the 8th degree polynomial with those coefficients gives you 511.
We can use the method suggested here
https://brilliant.org/wiki/method-of-differences/
By creating a difference table and note that D 8 ( n ) is a constant which is = 1
The wiki really helped me.
The sequence x n = a 0 + a 1 n + ⋯ + a 8 n 8 can be considered a linear combination of the sequences 1 , n , n 2 , ⋯ , n 8 . Using what is explained in the wiki Linear Recurrence- repeated roots, we obtain that the sequence ( x n ) n satisfies a linear recurrence with characteristic polynomial ( r − 1 ) 9 . Therefore we have that for any natural number n ≥ 9 , the following is always true k = 0 ∑ 9 ( k 9 ) ( − 1 ) k x n − k = 0 . Now, making n = 9 and solving for x 9 , we get x 9 = − k = 1 ∑ 9 ( k 9 ) ( − 1 ) k x 9 − k = − k = 1 ∑ 9 ( k 9 ) ( − 1 ) k 2 9 − k = 2 9 − ( 2 − 1 ) 9 = 5 1 1 .
A polynomial of the 8th degree sounds scary, so we should start with simpler cases.
To begin with, look at the polynomial of 1st degree (a line) given that f ( i ) = 2 i for i=0,1. This obviously generates a line with equation y = x + 1 , and f(2) in this case (since we're looking for f(n+1) where n is the degree of the polynomial) = 3.
Next, we examine the case with a polynomial of degree 2, or a quadratic, given that f ( i ) = 2 i for i=0,1,2. Solving the system of 3 equations with 3 variables, we find that f ( x ) = 0 . 5 x 2 + 0 . 5 x + 1 , and f(3) = 7.
We're beginning to see a pattern here, of f(n+1), where the polynomial has degree of n, has a value of 2 n + 1 − 1 , but let's do another one to make sure. Again, we have a polynomial, this time of degree 3 and having f ( i ) = 2 i for i=0,1,2,3. Solving the system of 4 variables and 4 equations, we get that f ( x ) = x 3 / 6 + 5 x / 6 + 1 , and f(4) = 15, which is equal to 2 4 − 1 .
We now hypothesize that f(9) in the original problem follows our formula, thus f ( 9 ) = 2 9 − 1 = 5 1 2 − 1 = 5 1 1 , giving us the final answer of 511.
f(x)=1-7x+22x^2-40x^3+46x^4-34x^5+16x^6-4x^7+x^8) f(9)=511 because all but one (namely 1+1+1+...+1=10) of the 2^9 compositions of 10 are in nine or fewer parts. Sum C(n,k), k=0..8 series
1st, we will assume that the graph from points x={0,1,2,3,4,5,6,7,8} is exponential satisfying the equation f(x)=2^x.
So at point when x=8, the graph will have its turning point and change the direction of its graph satisfying the equation f(y)=2^y with origin at point (8,512). Now, by using f(y)=2^y, let y=0 resulting to x=1. Going back to the graph, we will have to subtract 512 by the value of x which is 1 resulting to the value now of f(9) equal to 511.
Correct answer obtained by accident, the argument is totally wrong.
Fully agree with u Calvin
f(9)=Σ(2^i) (i=0 to 8)=2^9 -1=511
since it follows the general pattern given by them,f(0)=1. thus we found that the constant in the polynomial is 1. now f(9)=2^9-constant polynomial=512-1=511.
We can construct a finite difference table: f ( 0 ) 1 1 f ( 1 ) 2 1 2 1 f ( 2 ) 4 2 1 4 2 1 f ( 3 ) 8 4 2 1 8 4 2 1 f ( 4 ) 1 6 8 4 2 1 1 6 8 4 2 f ( 5 ) 3 2 1 6 8 4 3 2 1 6 8 f ( 6 ) 6 4 3 2 1 6 6 4 3 2 f ( 7 ) 1 2 8 6 4 1 2 8 f ( 8 ) 2 5 6 This last row has to be constant, so we can extend the finite difference table: f ( 0 ) 1 1 f ( 1 ) 2 1 2 1 f ( 2 ) 4 2 1 4 2 1 f ( 3 ) 8 4 2 1 8 4 2 1 f ( 4 ) 1 6 8 4 2 1 1 6 8 4 2 f ( 5 ) 3 2 1 6 8 4 1 3 2 1 6 8 3 f ( 6 ) 6 4 3 2 1 6 7 6 4 3 2 1 5 f ( 7 ) 1 2 8 6 4 3 1 1 2 8 6 3 f ( 8 ) 2 5 6 1 2 7 2 5 5 f ( 9 ) 5 1 1 Therefore, f ( 9 ) = 5 1 1 .