Polynomial twister
Let x 1 , x 2 , … , x 2 0 1 5 be the roots of the equation x 2 0 1 5 + x 2 0 1 4 + x 2 0 1 3 + … + x 2 + x + 1 = 0 . Evaluate
1 − x 1 1 + 1 − x 2 1 + … + 1 − x 2 0 1 5 1 .
The answer is 1007.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
We will find a polynomial with roots
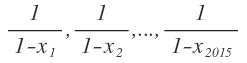
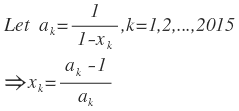
Since
 is a root of
is a root of
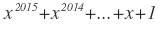

Moderator note:
There's a much simpler approach to this.
Hint : Consider the reciprocal of the roots of the given equation first. Alternatively, apply roots of unity.
And of course, can you generalize this?
Yes we can generalize this. Replace 2015 by n and the answer will be n/2.
I think this I solved this in an easier way.
Since this is a monic polynomial, we can say that
f ( x ) = x 2 0 1 5 + x 2 0 1 4 + … + x 2 + x + 1 = ( x − x 1 ) ( x − x 2 ) … ( x − x 2 0 1 5 )
f ( 1 ) = i = 1 ∏ 2 0 1 5 ( x − x i ) = 2 0 1 6
⇒ f ′ ( x ) = 1 . ( x − x 2 ) . ( x − x 3 ) … ( x − x 2 0 1 5 ) + ( x − x 1 ) . 1 . ( x − x 3 ) … ( x − x 2 0 1 5 ) + … + ( x − x 1 ) . ( x − x 2 ) … ( x − x 2 0 1 4 ) . 1
The above step was achieved by product rule .
f ′ ( x ) = 2 0 1 5 x 2 0 1 4 + 2 0 1 4 x 2 0 1 3 + … + 2 x + 1
⇒ f ′ ( 1 ) = j = 1 ∑ 2 0 1 5 j = ( 1 − x 2 ) . ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) + ( 1 − x 1 ) . ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) + … + ( 1 − x 1 ) . ( 1 − x 2 ) … ( 1 − x 2 0 1 4 )
The expression can be written as:
E = ∏ i = 1 2 0 1 5 ( 1 − x i ) ( 1 − x 2 ) . ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) + ( 1 − x 1 ) . ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) + … + ( 1 − x 1 ) . ( 1 − x 2 ) … ( 1 − x 2 0 1 4 )
⇒ E = f ( 1 ) f ′ ( 1 )
⇒ E = 2 0 1 6 ∑ j = 1 2 0 1 5 j = 2 0 1 6 2 2 0 1 5 . 2 0 1 6 = 1 0 0 7 . 5
Note:
a . b is the same as a × b
Moderator note:
Yes, you have the ideas for this.
I think that the easier approach is to realize we want to find the polynomial whose roots are of the form ( 1 − x i ) , and then find the sumproduct of all but 1 (2nd last coefficient), and product of all (last coefficient).
x 2 0 1 5 + x 2 0 1 4 + x 2 0 1 3 + … + x 2 + x + 1 = 0
From the equation above we have
a 1 = x 1 + x 2 + x 3 + … + x 2 0 1 5 = − 1
a 2 = x 1 x 2 + x 1 x 3 + x 1 x 4 + … + x 2 0 1 4 x 2 0 1 5 = 1
a 3 = x 1 x 2 x 3 + x 1 x 2 x 4 + … + x 2 0 1 3 x 2 0 1 4 x 2 0 1 5 = − 1
⋅
⋅
⋅
a 2 0 1 5 = x 1 x 2 x 3 x 4 … x 2 0 1 4 x 2 0 1 5 = − 1
a n = { 1 − 1 if n is even if n is odd
Let
A = 1 − x 1 1 + 1 − x 2 1 + … + 1 − x 2 0 1 5 1
A = ( 1 − x 1 ) ( 1 − x 2 ) ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) ( 1 − x 2 ) ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) + ( 1 − x 1 ) ( 1 − x 3 ) … ( 1 − x 2 0 1 5 ) + … + ( 1 − x 1 ) ( 1 − x 2 ) … ( 1 − x 2 0 1 4 )
A = 1 − a 1 + a 2 − a 3 + … + ( − 1 ) n a n + … − a 2 0 1 5 2 0 1 5 − 2 0 1 4 a 1 + 2 0 1 3 a 2 + 2 0 1 2 a 3 + … + ( − 1 ) n ( 2 0 1 5 − n ) a n + … + a 2 0 1 4
A = 1 + 1 + 1 + … + 1 + 1 2 0 1 5 + 2 0 1 4 + 2 0 1 3 + … + 2 + 1
A = 2 0 1 6 2 0 3 1 1 2 0
A = 1 0 0 7 . 5
You don't need to calculate 2031120. Your third last step is A = 1 + … + 1 2 0 1 5 + … + 1 = 2 0 1 6 2 1 ⋅ 2 0 1 5 ⋅ 2 0 1 6 = 2 2 0 1 5 .
My solution to this problem is just a matter of keen observation.
Consider 1 − x 1 1 + 1 − x 2 1 , which can be written as 1 − ( x 1 + x 2 ) + x 1 x 2 2 − ( x 1 + x 2 )
Observe the coefficients of the Numerator : 2 and − 1
Observe the coefficients of the Denominator : 1 , − 1 and 1
Please have a note of the terms in the expression too... ( e 1 and e 2 ) are the terms
Now consider 1 − x 1 1 + 1 − x 2 1 + 1 − x 3 1 which can be written as
1 − ( x 1 + x 2 + x 3 ) + ( x 1 x 2 + x 2 x 3 + x 1 x 3 ) − x 1 x 2 x 3 3 − 2 ( x 1 + x 2 + x 3 ) + ( x 1 x 2 + x 2 x 3 + x 1 x 3 )
→ Observe the coefficients of the Numerator : 3 , − 2 and 1
→ Observe the coefficients of the Denominator : 1 , − 1 , 1 and − 1
1 − ( x 1 + x 2 + x 3 ) + ( x 1 x 2 + x 2 x 3 + x 1 x 3 ) − x 1 x 2 x 3 3 − 2 ( x 1 + x 2 + x 3 ) + ( x 1 x 2 + x 2 x 3 + x 1 x 3 ) can be written as 1 − e 1 + e 2 − e 3 3 − 2 e 1 + 1 e 2
So for 2 0 1 5 such terms, the coefficients in Numerator will be 2 0 1 5 , − 2 0 1 4 , 2 0 1 3 , − 2 0 1 2 . . . − 2 , 1
And coefficients of denominator will be 1 , − 1 , 1 , − 1 . . . . 1 , − 1
So obviously the the expression of the question could be written as
1 − e 1 + e 2 − e 3 + . . . − e 2 0 1 5 2 0 1 5 − 2 0 1 4 e 1 + 2 0 1 3 e 2 − 2 0 1 2 e 3 + 2 0 1 1 e 4 − . . . − 2 e 2 0 1 3 + 1 e 2 0 1 4 − 0
Where,
→ e 1 = ∑ x 1 = − 1
→ e 2 = ∑ x 1 x 2 = 1
→ e 3 = ∑ x 1 x 2 x 3 = − 1 and so on until
→ e 2 0 1 5 = x 1 x 2 . . . x 2 0 1 5 = − 1
Therefore, we get 1 + 1 + 1 . . . . + 1 ( 2 0 1 6 times) 2 0 1 5 + 2 0 1 4 + 2 0 1 3 + . . . + 2 + 1
= 2 ( 2 0 1 6 ) ( 2 0 1 5 ) ( 2 0 1 6 ) = 2 2 0 1 5 = 1 0 0 7 . 5
For simplicity, let N : = 2 0 1 5 and define the monic polynomial P ( x ) : = k = 0 ∑ N x k = k = 1 ∏ N ( x − x k ) , x k : roots of P ( x ) , P ( 1 ) = N + 1 = 0 If we take the derivative P ( 1 ) ( x ) , the product formula always cancels exactly one factor of P ( x ) . With P ( 1 ) = 0 we may write k = 1 ∑ N 1 − x k 1 = P ( 1 ) P ( 1 ) ( 1 ) = N + 1 ∑ k = 0 N k ⋅ 1 k − 1 = 2 ( N + 1 ) N ( N + 1 ) = 2 N = 1 0 0 7 . 5
note that x is 2016th root of unity which means that | x| = 1; now let x be a non-real root, then x conjugate must also be a root, now note pair all of the terms with their conjugate and upon summing each pair you will get 1007. Then note that for the last lone term its value is just 1/2 = 0.5 thus answer is 1007.5
Notice that x sub 1008 is -1 while x sub (1008+k) and x sub (1008-k) are conjugates in the complex plane with magnitude 1. We can then find out that 1/(1-z1) + 1/(1-z2) where z1 and z2 are conjugates is equal to 1. Since 1/(1-x_1008) is equal to 1/2 and there are 1007 pairs of conjugates we have the sum is equal to 1007 + 1/2 or 1007.5
f ( x ) = x 2 0 1 5 + x 2 0 1 4 + x 2 0 1 3 + … + x 2 + x + 1
f ( 1 ) = 1 + 1 + 1 + … + 1 + 1 = 1 = 2 0 1 6
f ′ ( x ) = 2 0 1 5 x 2 0 1 4 + 2 0 1 4 x 2 0 1 3 + 2 0 1 2 x 2 0 1 3 + … + 2 x + 1
f ′ ( 1 ) = 2 0 1 5 + 2 0 1 4 + 2 0 1 3 + … + 2 + 1 = 2 2 0 1 5 × ( 1 + 2 0 1 5 ) = 2 2 0 1 5 × 2 0 1 6
We have other form of f ( x )
f ( x ) = ( x − x 1 ) ( x − x 2 ) … ( x − x 2 0 1 5 )
lo g f ( x ) = lo g ( x − x 1 ) ( x − x 2 ) … ( x − x 2 0 1 5 )
f ( x ) f ′ ( x ) = x − x 1 1 + x − x 2 1 + … + x − x 2 0 1 5 1
f ( 1 ) f ′ ( 1 ) = 1 − x 1 1 + 1 − x 2 1 + … + 1 − x 2 0 1 5 1
2 0 1 6 2 2 0 1 5 × 2 0 1 6 = 1 − x 1 1 + 1 − x 2 1 + … + 1 − x 2 0 1 5 1
1 − x 1 1 + 1 − x 2 1 + … + 1 − x 2 0 1 5 1 = 1 0 0 7 . 5