Polynomial Wire Dynamics
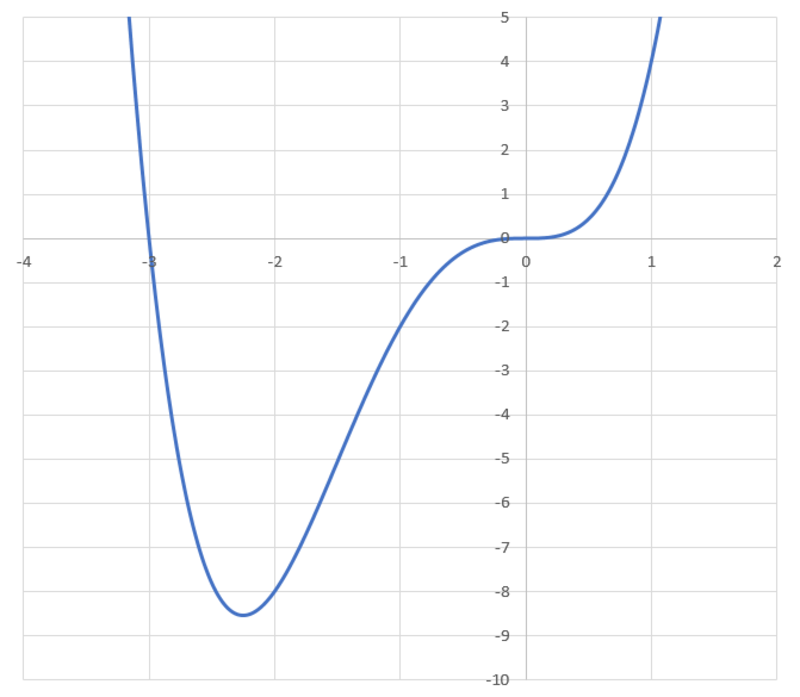
A bead of mass m is confined to a smooth wire in the shape of the curve y = x 4 + 3 x 3 . The bead experiences a constant gravitational force of m g in the negative y direction. The bead begins at rest at time t = 0 and position x = 1 . If a ( t ) is the instantaneous magnitude of the bead's acceleration, and T is the period of motion, determine the following integral.
I = ∫ 0 T a ( t ) d t
Details and Assumptions:
- m = 1
- g = 1 0
The answer is 195.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Here's my approach which avoids tedious differentiation:
Since the beam is forced to move along the wire, we have: v ˙ = v ˙ T ^ + v T ^ ˙ = v ˙ T ^ + v d s d T ^ d t d s = v ˙ T ^ + v 2 d s d T ^ Here, v is speed, v ˙ is the tangential acceleration and d s d T ^ is the curvature vector, which is normal to tangent line. If we denote θ to be the angle between the tangent line and x-axis, we have: v ˙ d s d T ^ = g sin ( θ ) = g 1 + tan 2 θ tan θ = g 1 + y ′ 2 y ′ = κ N ^ = ( 1 + y ′ 2 ) 2 3 y ′ ′ N ^ It follows that the squared magnitude of acceleration is, by Pythagorean theorem: ∥ a ∥ 2 = g 2 1 + y ′ 2 y ′ 2 + v 4 ( 1 + y ′ 2 ) 3 y ′ ′ 2 We can write this whole expression as a function of x , which then becomes: ∥ a ∥ 2 = g 2 1 + ( 4 x 3 + 9 x 2 ) 2 ( 4 x 3 + 9 x 2 ) 2 + 4 g 2 ( 4 − x 4 − 3 x 3 ) 2 ( 1 + ( 4 x 3 + 9 x 2 ) 2 ) 3 ( 1 2 x 2 + 1 8 x ) 2 = g 2 x 2 [ 1 + x 4 ( 4 x + 9 ) 2 ( 4 x + 9 ) 2 + 1 4 4 ( 4 − x 4 − 3 x 3 ) 2 ( 1 + x 4 ( 4 x + 9 ) 2 ) 3 ( 2 x + 3 ) 2 ] I used the same arguments as you in the finish, but I get a slightly different result - 195.85619 - which is probably due to my imperfect method of numerical integration.
The position vector of the particle is r = ( x 4 + 3 x 3 x ) and hence r ˙ = ( 4 x 3 + 9 x 2 1 ) x ˙ r ¨ = ( 4 x 3 + 9 x 2 1 ) x ¨ + ( 1 2 x 2 + 1 8 x 0 ) x ˙ 2 Conservation of energy tells us that 2 1 ∣ ∣ r ˙ ∣ ∣ 2 + g ( x 4 + 3 x 3 ) = 4 g and hence x ˙ 2 = 1 + ( 4 x 3 + 9 x 2 ) 2 2 g ( 4 − 3 x 3 − x 4 ) and we differentiate to obtain x ¨ = d x d [ 1 + ( 4 x 3 + 9 x 2 ) 2 g ( 4 − 3 x 3 − x 4 ) ] Thus we can obtain the magnitude of the acceleration a = ∣ r ¨ ∣ as a function of x .
Solving the equation x 4 + 3 x 3 − 4 = 0 numerically, we deduce that the particle oscillates between x = 1 and x = α = − 3 . 1 3 0 3 9 5 . The desired integral is ∫ 0 T ∣ a ( t ) ∣ d t = 2 ∫ α 1 ∣ x ˙ ∣ a ( t ) d x = 1 9 5 . 9 8 2 after numerical integration.