Polynomials going crazy!

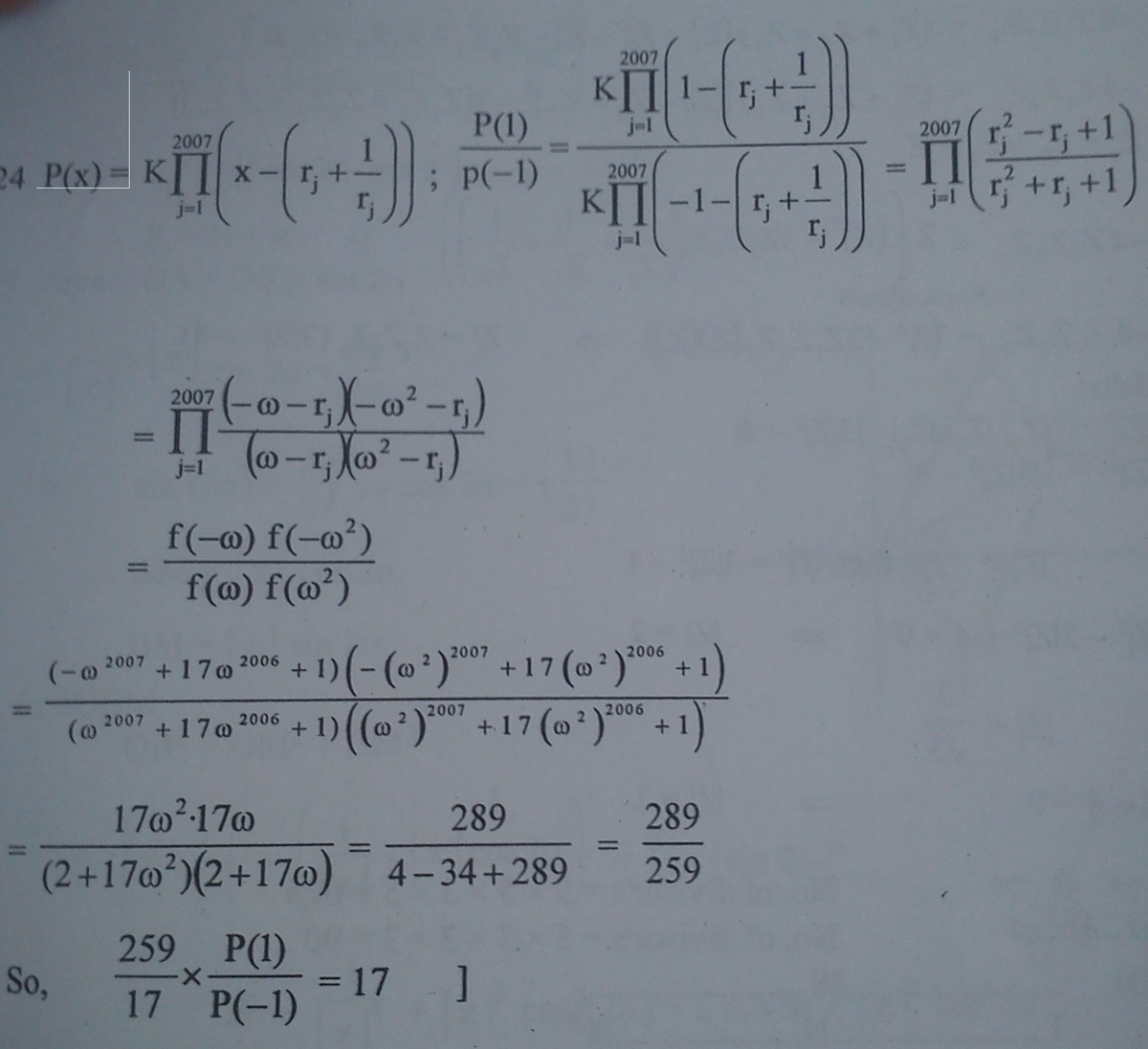
We can see that none of the roots of $f(x)$ is zero. So we can form a polynomial whose roots are the numbers $\frac{1}{r_j}$ for $j=1, 2, 3, ..., 2007$ and with 1 as leading coefficient just by considering $g(x)=x^{2007} f(\frac{1}{x})$ , and, additionally, $g(x)=\prod_{j=1}^{2007}(x-\frac{1}{r_j}).$

Since $P(x)=c\prod_{j=1}^{2007}(x-r_j-\frac{1}{r_j})$ where $c$ is a constant then, $\begin{aligned} P(x+\frac{1}{x})&=c\prod_{j=1}^{2007}(x+\frac{1}{x}-r_j-\frac{1}{r_j})\\ &=c \prod_{j=1}^{2007}\frac{(x-r_j)(x-\frac{1}{r_j})}{x}\\ &=c x^{-2007}f(x)g(x)\\ &=c f(x)f(\frac{1}{x})\end{aligned}.$

Now, since $e^{i\frac{\pi}{3}}+\frac{1}{e^{i\frac{\pi}{3}}}=1,$ $e^{i\frac{2\pi}{3}}+\frac{1}{e^{i\frac{2\pi}{3}}}=-1,$ and using the equality above, we obtain that $\frac{259}{17}\times \frac{P(1)}{P(-1)}=\frac{259}{17}\times \frac{P\left(e^{i\frac{\pi}{3}}+\frac{1}{e^{i\frac{\pi}{3}}}\right)}{P\left(e^{i\frac{2\pi}{3}}+\frac{1}{e^{i\frac{2\pi}{3}}}\right)}=\frac{259}{17}\times\frac{f(i\frac{\pi}{3})f\left(\frac{1}{e^{i\frac{\pi}{3}}}\right)}{f(e^{i\frac{2\pi}{3}})f\left(\frac{1}{e^{i\frac{2\pi}{3}}}\right)}$ $=\frac{259}{17}\times \frac{17^2}{259}=\boxed{17}.$