Polytrigonometry

Geometry Level 5

The least degree of a polynomial with integer coefficients whose one of the roots may be $\large{\cos(\frac{\pi}{15})}$ is?

5 3 15 4 None of these choices

2 solutions

Tanishq Varshney
May 4, 2015

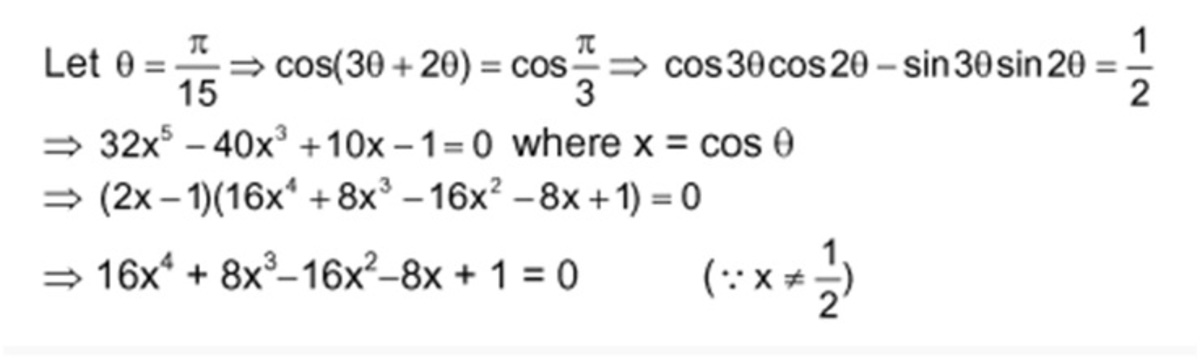
How can we conclude that this is the polynomial with "least" degree with integer coef. for this root.

Gaurav Jain - 6 years, 1 month ago

Alan Enrique Ontiveros Salazar
May 19, 2015

There is a theorem that says if $x=\cos \left(\dfrac{2\pi k}{n}\right)$ , where $\text{gcd}(k,n)=1$ , then the minimal polynomial of $x$ is of degree $\dfrac{\varphi(n)}{2}$ , where $\varphi(n)$ is the Euler's Totient Function.

So, in this case, $x=\cos\left(\dfrac{2 \pi k}{30}\right)$ , where $k=1$ and $n=30$ , and the minimal polynomial of $x$ is then $\dfrac{\varphi(30)}{2}=\boxed{4}$ .

Polytrigonometry

2 solutions

0 pending reports