Points and regions

Probability Level 1

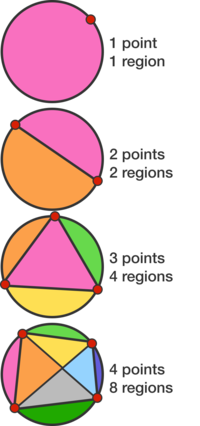
Select a number of points along the circumference of a circle and connect each pair with a chord. These chords will divide the interior of the circle into a number of regions.

The maximum numbers of regions are shown at right for 1 to 4 points.

What is the maximum number of regions for six points?

12 16 31 32 64

3 solutions

David Vreken
Oct 4, 2018

This is a classic problem demonstrating the dangers of inductive reasoning, because although it appears that the maximum number of regions $R$ and the the number of points along the circumference of the circle $n$ are related by the equation $R = 2^{n - 1}$ , it is actually related by the equation $R = 1 + {n \choose 2} + {n \choose 4}$ , $1$ for the starting region of the circle, ${n \choose 2}$ for the number of possible chords that can be drawn (each new chord adds a new region), and ${n \choose 4}$ for the number of possible quadrilaterals that can be drawn (each new quadrilateral has two intersecting diagonals that adds a new region).

For $n = 6$ points, the maximum number of regions is therefore $R = 1 + {6 \choose 2} + {6 \choose 4} = 1 + 15 + 15 = \boxed{31}$ , as illustrated below.

6 outer ring, 6 "star tips" bisected=12, 6 between tips, 6 inner edge of hexagon, 1 in center, 6x5+1=31

mike c - 2 years, 7 months ago

Kazi Abu Rousan
Oct 17, 2018

The most beautiful solution is the 3blue 1 brown video see this and all will be clear [https://youtu.be/K8P8uFahAgc]

Whoever runs this channel is a genius.

Rn munjal - 2 years, 5 months ago

[https://youtube/K8P8uFahAgc]

Lâm Lê - 9 months ago

Dennis Rodman
Oct 14, 2018

This should be under "Intermediate" instead, especially given that the case asked for was only for n = 6 and that the answer choices were supplied.

Why don't you give this in a report?

Syed Hamza Khalid - 2 years, 7 months ago

Use Euler’s formula for planar graphs, vertices - edges + faces = 2. For edges, take a vertex and call it 1 and label the other verticies on the circle clockwise. From vertex 1, you have an edge (1,2) and (1,6). For chord (1,3), you have three lines crossing it from vertex 2 to side 4,5,6 and this generates 4 edges. Same for the chord from 1 to 5. The chord from 1 to 4 is cut by two chords (2,5) and (2,6) and by two chords (3,6) and (3,5) and so the chord from 1 to 4 has 5 edges. Total edges are 1+1+4+4+5 = 15. For the 6 vertices, the total edges are 6*15=90 with edges double counted for each direction of a chord; i.e. (a,b) and (b,a) and so unique edges are 90/2=45. The number of vertices = 6 on the circle + the number of internal chord intersection (6 choose 4) = 6+15=21. Using Euler’s formula, 45-21+faces=2, gives 26 faces but it counts the area outside the graph as a face so the internal graph faces = 26-1=25. Adding the 6 areas between the circumscribed circle and the 6 chords on the outer edges of the planar graph gives 25+6=31 faces.

Phil Lawroski - 2 years, 7 months ago

Points and regions

3 solutions

0 pending reports