Pool Math
 In a pool party, you decide to test your mad Math skills.
In a pool party, you decide to test your mad Math skills.
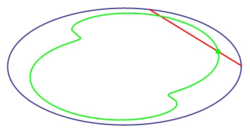
Having nothing better to do, you place a rigid iron bar inside a section c of an empty pool such that either end of it lies on the same plane and touch the insides of the pool. You then choose a point P on the bar such that the distance to one end is 7 and the distance to the other end is 3 , with the length of the bar being 10 . Finally, you move the bar in a way that, at any given time, neither end leaves c .
Suppose that each pool is a surface such that its horizontal sections are convex closed curves.
After one lap - at the moment the bar is back where it was first placed - what is the area between the curve covered by point P and the border of c , rounded to the closest integer?
The answer is 66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, look here .
As shown in the figure above, we assume that, as the bar moves, it is always tangent to a given curve e inside of the original section - and this curve is not the curve described by point P. Let Q be the point at which the bar is tangent to e , A and B be the points at each end of the bar and r the distance from A to Q. We then use the fact that the area of a tangent sweep equals the area of a tangent cluster ( Mamikon's Theorem , probably not the most famous of theorems) to say that the area covered by a given tangent cluster is:
∫ 0 2 π ∫ 0 k ( θ ) R d R d θ = 2 1 ∫ 0 2 π k 2 ( θ ) d θ
Instead of solving for numbers, I'll suppose segment AP has length a and segment PB has segment b, for a total of a+b. We can then write three integrals:
1) The area covered by segment AQ
I A Q = 2 1 ∫ 0 2 π r 2 d θ
2) The area covered by segment BQ
I B Q = 2 1 ∫ 0 2 π ( a + b − r ) 2 d θ
3) The area covered by segment PQ
I P Q = 2 1 ∫ 0 2 π ( a − r ) 2 d θ
Notice that segments AQ and BQ sweep the same area, which means I A Q = I B Q . Notice also that if we take the area swept by BQ minus the area swept by PQ, we get the area swept by PB - which is what we wanted in the first place. Therefore:
A = I B Q − I P Q = 2 1 ∫ 0 2 π ( a + b − r ) 2 − ( a − r ) 2 d θ = 2 1 ∫ 0 2 π ( 2 a b + b 2 − 2 b r ) d θ
However, r depends on \theta; we then use our previous relation
I A Q = I B Q
which yields
∫ 0 2 π r d θ = π ( a + b ) .
Finally, we substitute this last integral on A:
A = 2 1 ∫ 0 2 π ( 2 a b + b 2 − 2 b r ) d θ = 2 π a b + π b 2 − π a b − π b 2 = π a b
Therefore, A = π a b . This is called Holditch's Theorem .
Choosing a=3 and b=7, we get A = π × 3 × 7 = 6 5 . 9 7 3 4 4 . . . ≈ 6 6 .