Pool Party Problem

First, lets find out a little more about our pool. The area of the pool is $100π$ , therefore $A=πr^2=100π \Longrightarrow r=10$ .

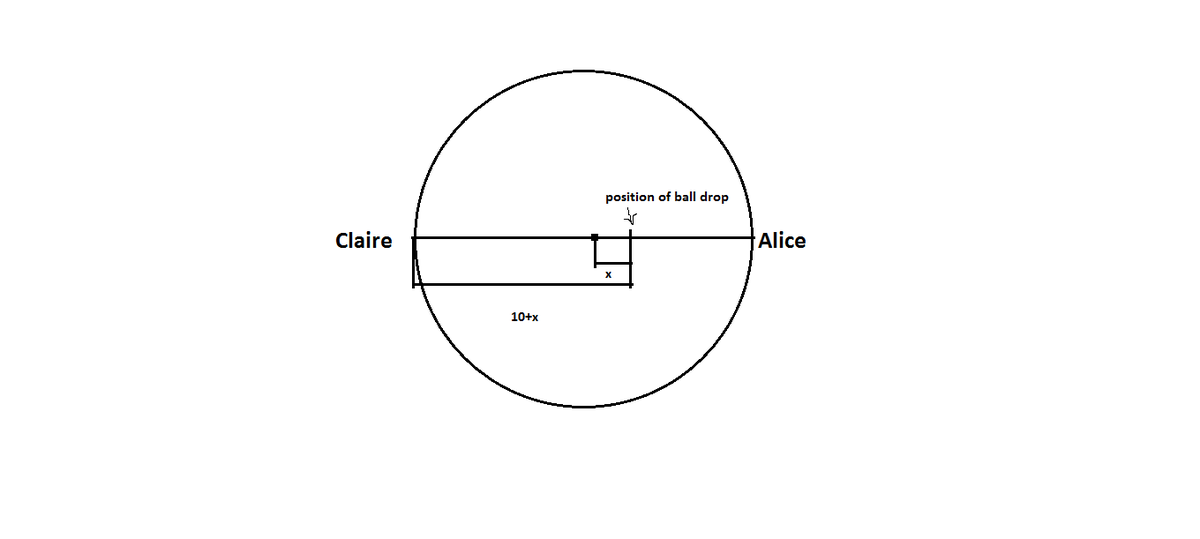
Second, let's talk about the lengths that each child has to swim in order to reach the ball. If Bobby swims twice as fast as Alice, then Bobby therefore should have to swim twice as far to reach the ball. Same for Carla, she has to swim twice as far as Bobby, and therefore 4 times as much as Alice to reach the ball. Observe the image below.

Our goal is to find the minimum value of $a$ such that the lines of length $10-a$ , $20-2a$ , and $40-4a$ can be drawn.

Let's now make some observations based on the situation. Let's say that the ball was thrown in the exact middle of the pool. If Alice and Carla are both on the edge of the pool, Carla will clearly get there first because both girls have to swim 10 ft. to get there. This establishes that there is a lower bound on $a$ . Our goal is to find that lower bound.

What would happen if we made $a$ big? We can imagine that Alice's dad wants her to have the ball, so he throws it right next to her. In order for Bobby and Carla to have a chance, they would have to be pretty close to Alice. The closer that the ball is thrown to Alice, the closer Bobby and Carla have to be to her, and the opposite then must be true as well; the farther that the ball is thrown from Alice (AKA the smaller the value of $a$ ), the farther away from Alice they both need to be.

Based on our observations, we can see that smaller values of $a$ leads to a greater distance between Alice and Carla. This however isn't an infinite pool, it has a boundary. If Alice and Carla reach the point where they are farthest from each other, a further decrease in $a$ can't lead to an increase in the distance between them, meaning that we've reached our boundary. So how far can Alice get from Carla? Well this question is trivial, Alice and Carla would have to be opposite each other, AKA they would have to be the endpoints on the diameter of the pool. We know from above that the radius of the pool is $10$ ft, so the diameter is $20$ ft. If Alice needs to travel $10-a$ ft and Carla needs to travel $40-4a$ ft, and their paths both outline the diameter of the circle, then all we should have to do is solve the equation $(10-a)+(40-4a)=20$ for $a$ and we're done.

$(10-a)+(40-4a)=20$

$50-5a=20$

$5a=30$

$a=\boxed{6}$

Here to get the minimum distance of the ball drop from the center(x).. Claire and Alice needed to be at opposite corner(For Claire to travel max distance and for Alice to travel min distance respective of their speeds)... So now (10+x)=(4)*(10-x) as Claire is 4 times faster than Alice, reaches at same time.. So 5x=30...and x=6..