Pool Shark Shuffle

We can visualize the ball travelling in a straight line through a series of reflected pool tables, as shown below.

To reach the goal, the ball would need to travel 1 meter in a vertical direction and 5 meters in a horizontal direction at a 1:5 ratio. Therefore, since the ball hits the right side of the table after it has traveled 1 meter in the horizontal direction, the missing vertical direction can be found by solving the proportion $\frac{1}{5} = \frac{x}{1}$ , which is $x = \boxed{\frac{1}{5}}$ meters.

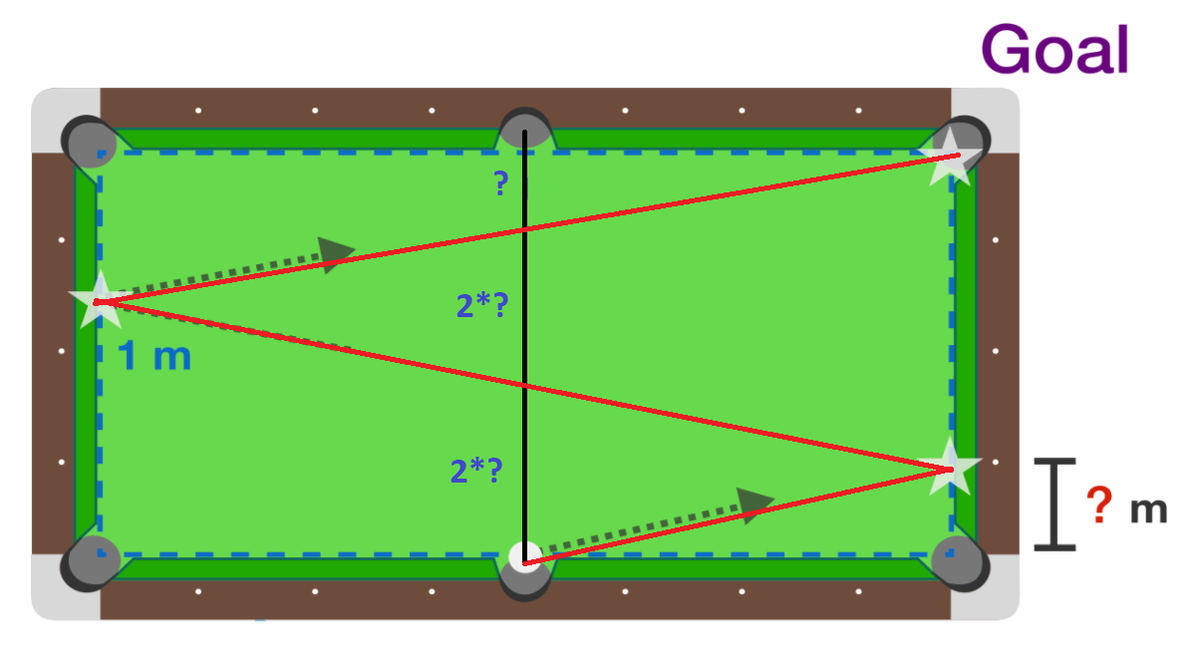
First, the ball goes towards the right side of the table, travelling $?\text{ m}$ upwards. Because the ball is reflected back at the same angle, once it travels the same distance, the ball's vertical height will increase by the same amount. Therefore, when the ball returns back to the middle, it will have travelled an additional $?\text{ m}$ upwards for a total of $2?\text{ m}$ .

Once the ball goes to the left side of the table and returns to the middle again, it will increase by $2?\text{ m}$ again. Finally, the hole will be on the right side of the table, so the ball's height will increase $?\text{ m}$ . These heights total to $5?\text{ m}$ , so $? = \frac{1}{5}\text{ m}$ .

If we consider the number of times the ball travels horizontally, it goes middle → right → middle → left → middle → right. This is a total of 5 movements, and the ball goes upwards by the same amount each time. Therefore, 5 times this upward amount = 1m, meaning $\frac{1}{5}$ is the answer.

EDIT: For clarity, this pattern of movements only works for the middle of the table. If say, the ball was only a quarter of the width from the first bounce, it would be 1 + 4 + 4 = 9 movements

I worked it it rather simply thinking about gradients. for every X meter traveled how many Y meters need to be traveled?

1) we know that in the Y direction total distance traveled is 1

2) total X distance is is 5 meters (1 meter from start to right edge, 2 meters for left edge to right and 2 meters from right to left)

gradient = rise/run gradient = 1/5 ( for every 1 meter in Y, 5 must be traveled in X)

and so ans = 1/5*1m = 1/5m

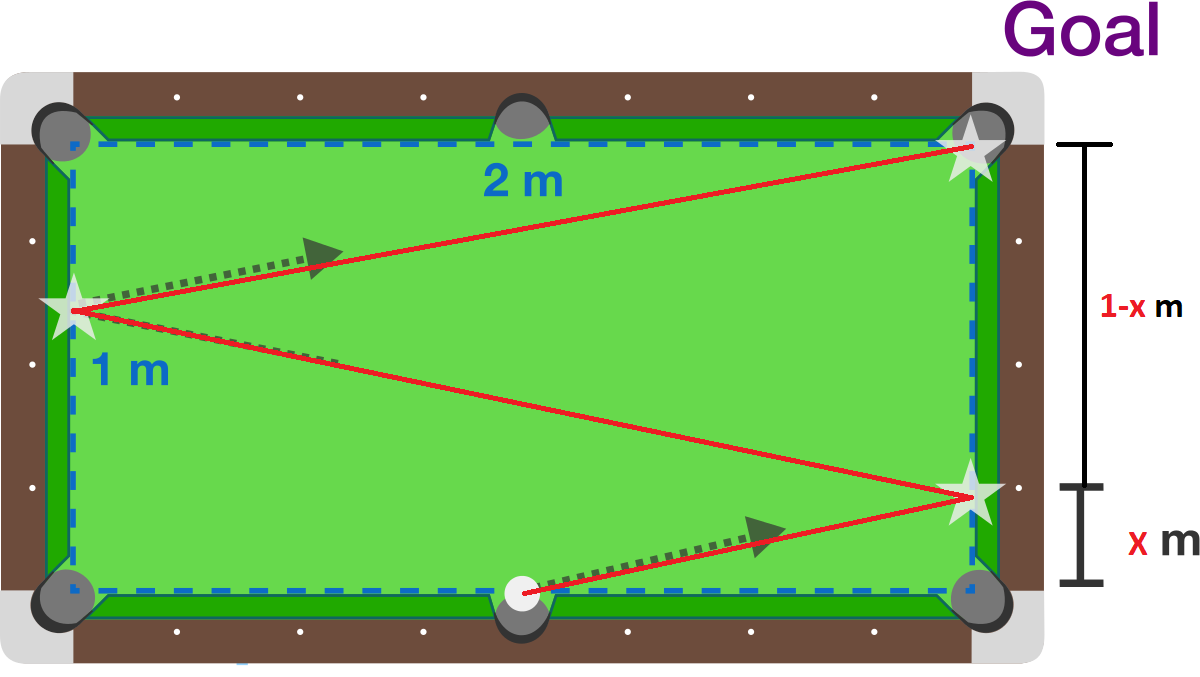
We begin by assigning lengths $x$ and $(1-x)$ in the picture above. Note that we are asked to find length $x.$

Now, represent the path we would like the ball to travel with red lines (as shown in the picture below).

Notice how in the picture above, we have formed a right triangle and an isosceles triangle. We will split the isosceles triangle into two right triangles by inserting an angle bisector (see image below).

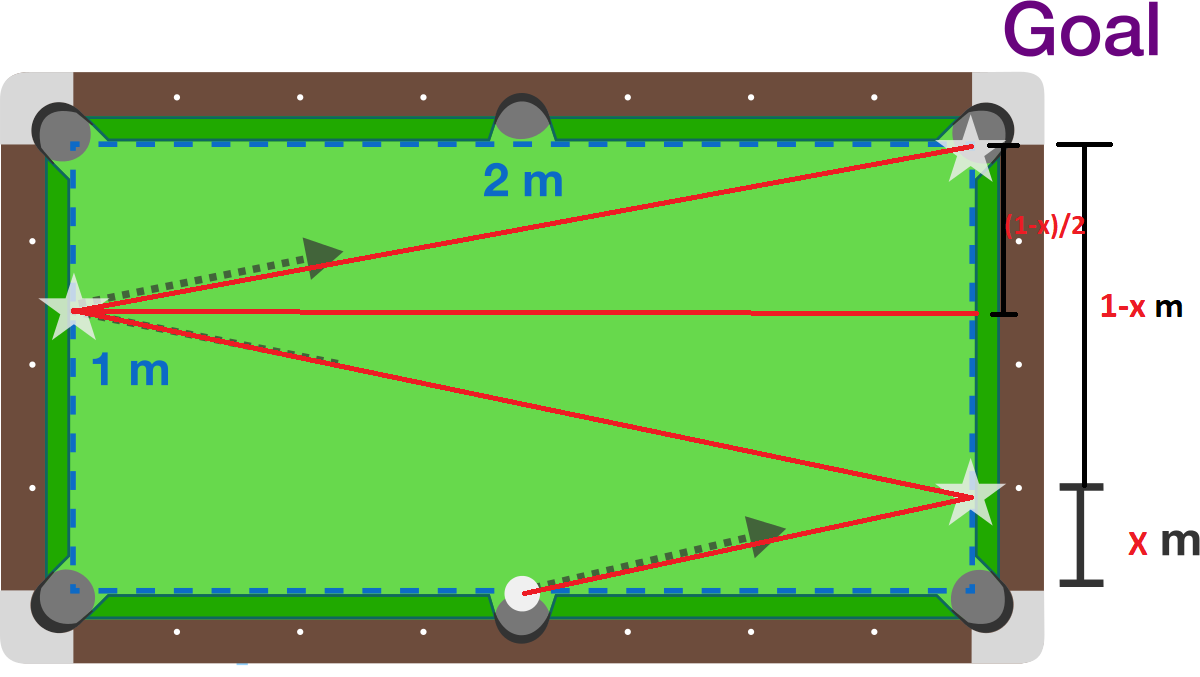
Note how the leg length of the top right triangle is now $\frac{(1-x)}{2}$ .

We will now assign letters to noteworthy points in the figure to make this solution easier to explain.

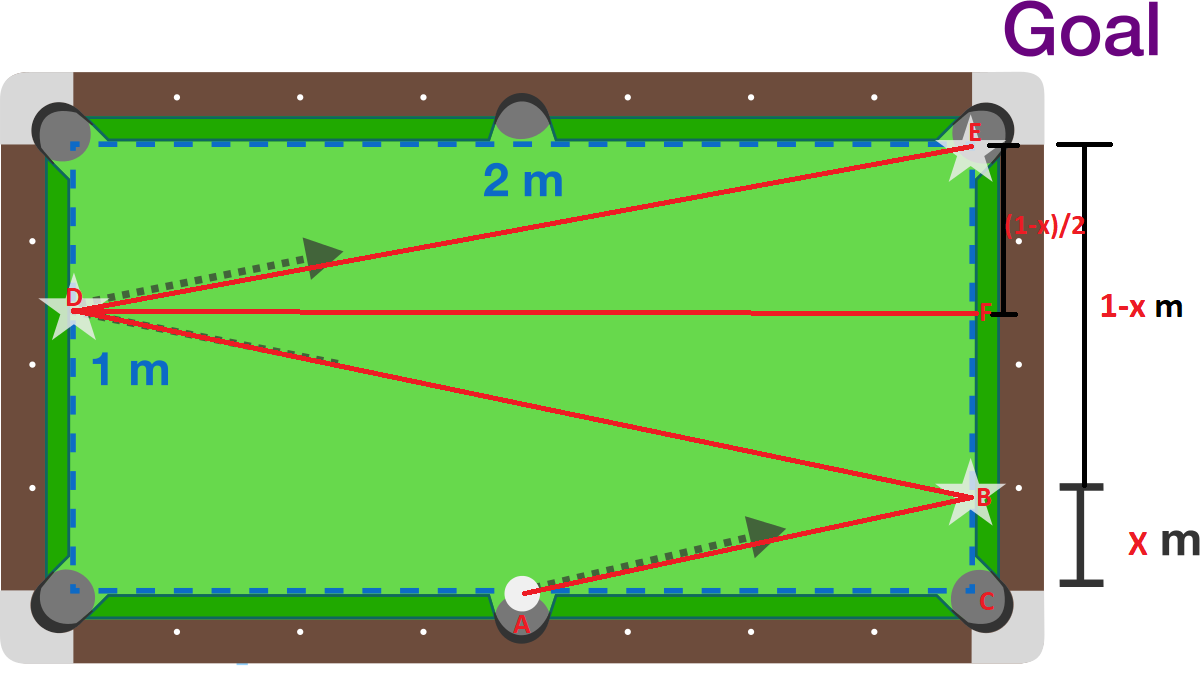
We now have everything we need to develop (and solve) a system of equations.

Triangle DEF has legs of length $2m$ and length $\frac{(1-x)}{2}$ .. We will use the pythagorean theorem to show that $(2)^2 + (\frac{1-x}{2})^2 = y^2$ where $y$ is the length of the hypotenuse of Triangle DEF.

Now, let's look at Triangle ABC. Length AB is parallel to length DE; however, length AB is only half as long. Since length DE was assigned length $y$ , we must assign length AB with a length of $\frac{y}{2}$ The image below depicts the current situation.

Note that the legs of triangle ABC are length x and length 1m. We will use the pythagorean theorem to show that $1 + x^2 = \frac{y^2}{4}$ .

We now have two equations:

Equation 1 . from Triangle DEF: $(2)^2 + (\frac{1-x}{2})^2 = y^2$

Equation 2 . from Triangle ABC: $1 + x^2 = \frac{y^2}{4}$

Equation 2 can be modified by multiplying each side of the equation by 4. The result is equation 3 : $4 + 4x^2 = y^2$

Since the left sides of equations 1 and 3 are both equal to $y^2$ , we will now set them equal to each other as follows:

$(2)^2 + (\frac{1-x}{2})^2 = 4 + 4x^2$

A little bit of algebra and simplification yields the following quadratic equation: $15x^2 + 2x - 1 = 0$

The roots of the equation are $(-1/3)$ and $(1/5)$ . In this context, a negative solution is nonsensical. Therefore, the correct solution is $x = 1/5$ meters.

In pool, the angle of incidence needs to equal the angle of reflection, or there'd be something wrong with the pool table itself. From the illustration, we see the first angle the ball takes when hitting the first bumper. Let's call that x. When the ball rebounds, we see it makes twice the original angle, or 2x, since it makes the first angle out the same angle it went in, which is equal to the angle the ball was shot at , or x. It then goes to the other side, and makes another double angle against the bumper over there, or 2x. Altogether, there are x+2x+2x, or 5 equal angles, requiring the ball to be shot at 1/5th the width of the table (1 meter), in order to fall in the upper right pocket. Thus, the answer as to where to aim one's shot to make the ball go the desired path would be at the 1/5th meter mark. ☺☺☺☺

It is 1/5 meters.

If we visualize the ball direction to the goal, we can realize that the angle (α) with which the ball bounces in the sides of the table is the same:

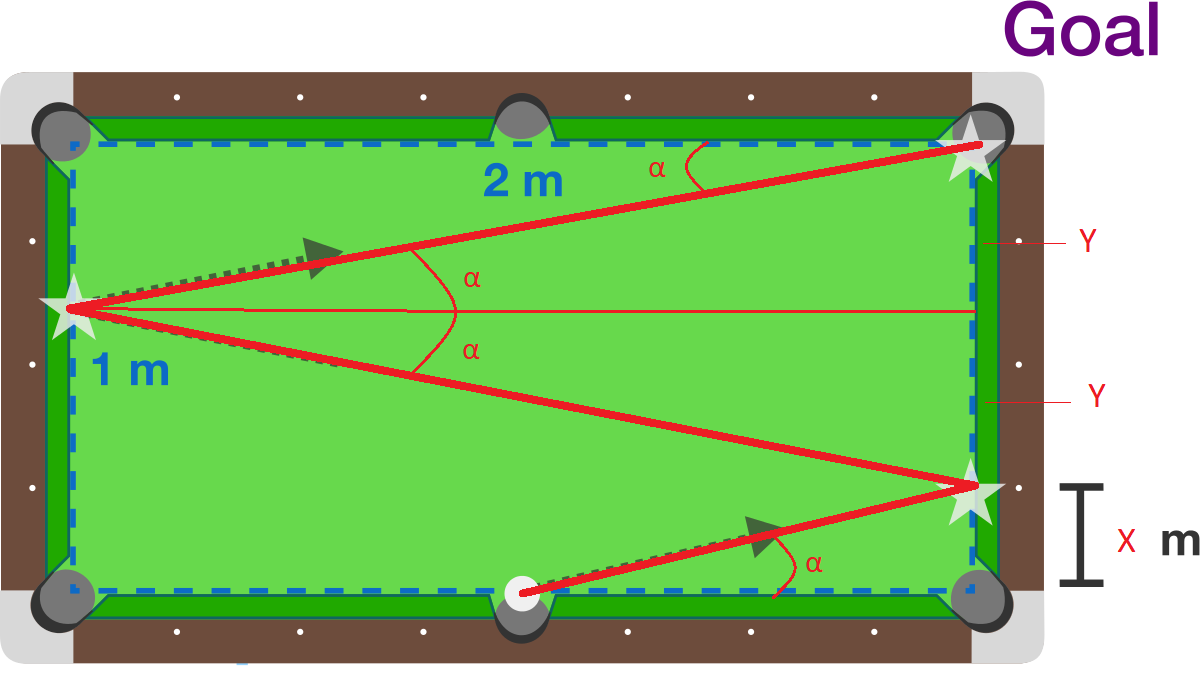
With this reasoning we can formulate 3 equations: Tan α = $\frac{x}{1}$ // Tan α = $\frac{y}{2}$ // 2y + x = 1 //. Equaling the 2 first we obtain the following wquation system: y = 2x // 2y + x =1 // And solving this we have: 4x + x =1 ➞ 5x = 1 ➞ x = $\frac{1}{5}$

Let $\alpha$ be the shot angle with respect to the horizontal where an angle of 0 degrees would be rightward.

Let $x_0$ be the value in meters of the first bounce (the answer we seek).

These are related by $x_0 = tan(\alpha)$ .

Given a sensible law of reflection and some trig, we can write a formula for the vertical position of all future bounces $x_n = (2n+1) tan(\alpha)$ .

$x_2$ (n=2) is where the ball falls into the hole (instead of bouncing) and we know its value in meters is 1 = $x_2 = 5tan(\alpha)$ and we can solve for $\alpha = tan^{-1}(\frac{1}{5})$

Therefore, $x_0 = \tan(tan^{-1}(\frac{1}{5}))=\frac{1}{5}$ .

I solved it using basic trigonometry.

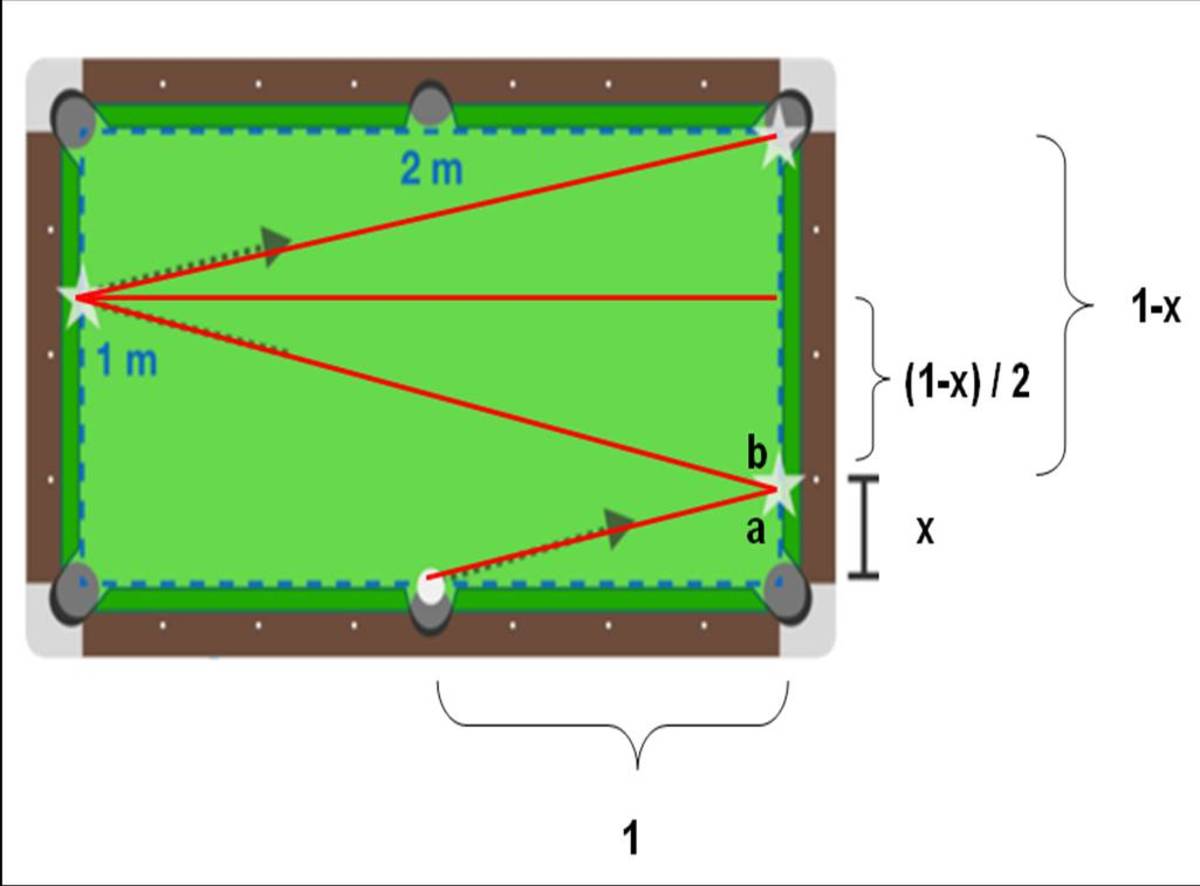
The tangent of angle a = $\frac{1}{x}$ The tangent of angle b = $\frac{2}{(1-x)/2}$ Now angle a = angle b. So we can say that: $\frac{1}{x}$ = $\frac{2}{(1-x)/2}$ ie $\frac{1}{x}$ = $\frac{4}{(1-x)}$ ie 1 - x = 4x so therefore x = $\frac{1}{5}$

We know 1m is width and 2m is length. The ball hits the 1m side at an angle then spans the length of the pool table twice. 2 is twice as large as 1. So 1/5 of the 1m at first hit, then by the time u get to your second hit, u will have covered 3/5 total is the width. And lastly as the ball is going back the same distance toward the goal it will complete 5/5 or the whole width of the table. If it we're a square (having equal sides) then each of the 2 hits will only cover 1/3 of the table. 1/x + 1/2x + 1/2x = 1 can be used to find what fraction of the width u have to hit

I was really confused for a moment because this quiz was trying to pocket the cue ball...