Portal Physics (Part 2)
The images below show two circular portals: Portal 1 (orange) on the floor with center at and Portal 2 (blue) on the wall with center at . Gravity is in the negative- direction.
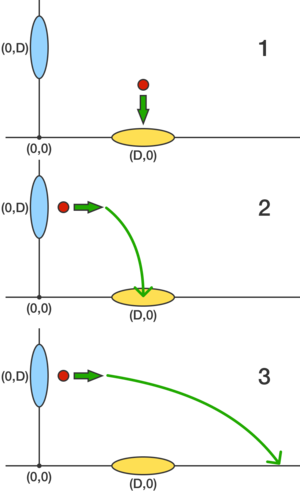
A ball is dropped from directly above the center of Portal 1. The height of the original drop is such that after the ball emerges from Portal 2, it again enters Portal 1 at its center. Upon emerging from Portal 2 the second time, the ball now overshoots Portal 1 and lands on the ground.
If the ball lands a distance of from the origin, what is the value of
(Also try Part 1 .)
Details and Assumptions: (These rules of portal physics are slightly revised from the previous problem.)
- An object enters one portal and emerges from the other.
- Portals do not conserve vector momentum or total energy (kinetic + potential).
- Portals do conserve the scalar speed of objects that enter/exit them.
- Objects always exit portals from the center, with velocity directed normally to the portal surface.
- Portals do not impart their own velocity to objects which pass through them.
- Aside from their own strange properties, portals do not otherwise alter the physics of nearby objects and environments.
- It takes zero time to go through a pair of portals.
The answer is 2.23607.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In the second frame, where the ball emerges from Portal 1 and enters the center of Portal 2 , the ball has an initial vertical velocity of zero which means its vertical distance is given by D = 2 1 g t 2 , which solves to t = g 2 D , and its vertical velocity when it reaches Portal 2 is given by v y = g t , which solves to v y = 2 D g . In this same amount of time t , the ball will also travel a horizontal distance D at a constant horizontal velocity v x at v x = t D , which solves to v x = 2 1 D g . Therefore, the scalar speed of the ball upon entering Portal 2 in the second frame is s = v x 2 + v y 2 = 2 1 D g 2 + 2 D g 2 = 2 5 D g .
In the third frame, where the ball emerges from Portal 1 and lands past Portal 2 , this scalar speed is converted to a horizontal velocity, so v x = s = 2 5 D g . Since the ball will fall the same distance as in the second frame, t = g 2 D once again, and the horizontal distance is d x = v x t = 2 5 D g g 2 D = 5 D . Therefore, the ball lands 5 D from the origin, so α = 5 ≈ 2 . 2 3 6 0 7 .