Position and Velocity
Calculus
Level
2
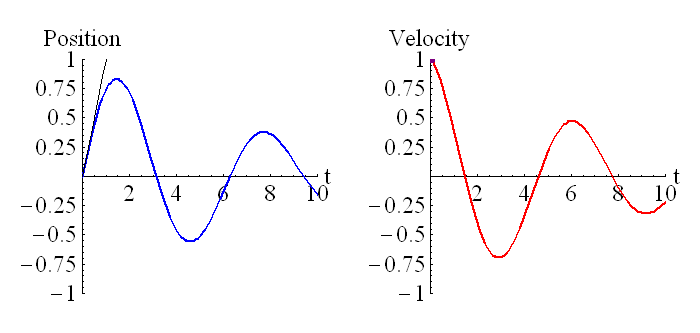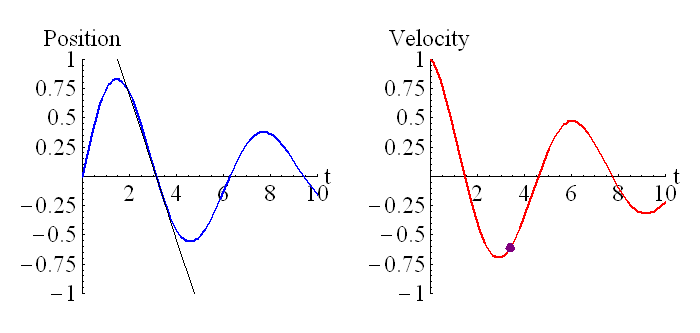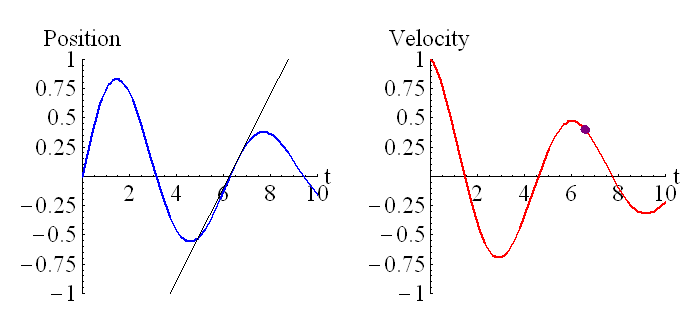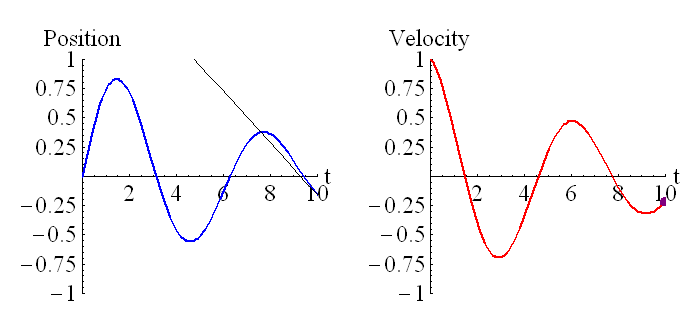The position is the integral of velocity. However, both position and velocity have different dimensions. So…how is this difference generally consistent with the conclusion that the integration sign is dimensionless?
After doing the integral, one of them should multiply by time to get position.
Integration sign carries units of time.
The integral equations don’t need to have the same dimensions on both sides.
Integration involves multiplication by a differential unit of time.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The general relationship between position and velocity is
x = \int {v} dt
Even though the integration sign is dimensionless, the factor of dt is a time, because it is a little bit of time. So, the relationship between the position’s dimensions and the velocity’s dimensions would be [x] = [v] x T as we generally would suppose to be.