Position of the antenna
So this is a nice one I had on a test at school. I'll try to describe it as best as I can remember.
Consider a straight road connecting two towns, town A and Town B. Between the Towns A and B there is point C. Distant 14 km from point C and perpendicular to the road there's an antenna, and it's signal ranges 15 kilometers. The antenna is used by the highway patrol for communication in the route between the town A and B, but neither town A, distant 9 km from point C, or Town B, distant 12 km from point C, can receive the signal of the antenna.
With the intent of both towns receive the signal of the antenna, they decided to move it the minimal necessary closer to point C. How much will they move the antenna?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This is a problem that requires trigonometry. According to the Pythagorean theorem, the sum of the squares of the lengths of the catheti is equal to the square of the length of the hypotenuse, shortly, a² + b² = c² Being town B the farthest to the antenna, it is what we should focus on. Giving point D as the position of the antenna, the catheti are the distance from point C to point D (14 km) and from point C to point B, or town B (12 km) Image for reference: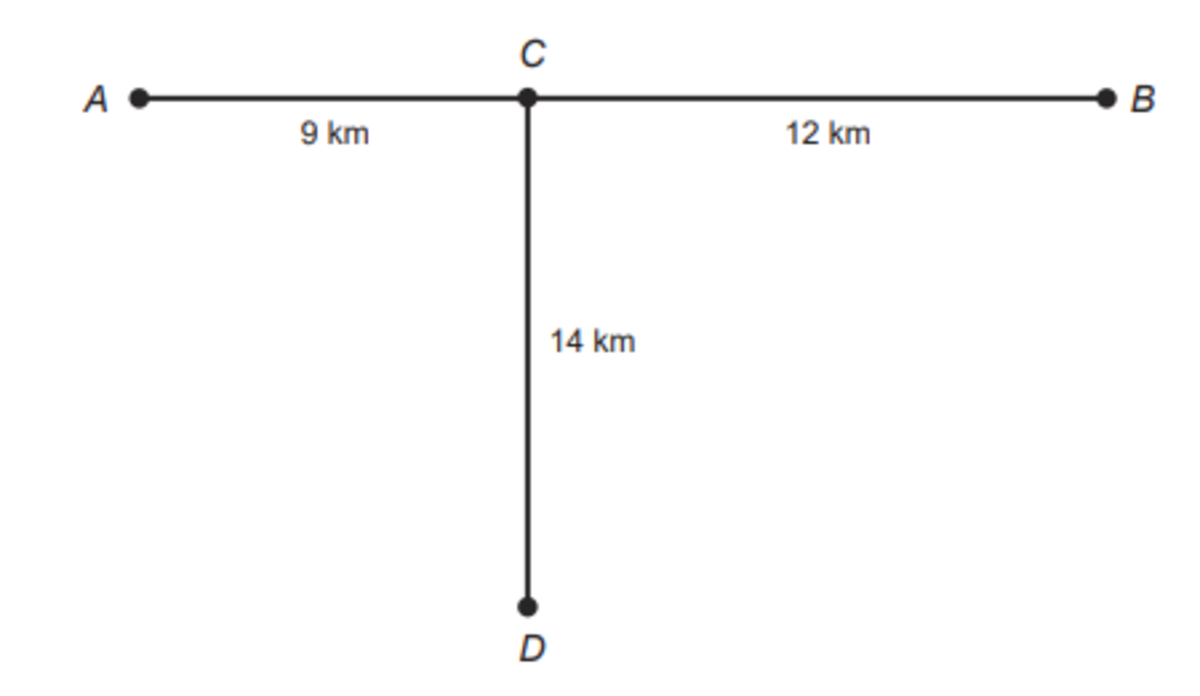
For the antenna to reach the farthest town, the maximum length of the hypotenuse should be 15; remember that the intent is to move the antenna the minimum necessary, so no less than that either, and to reach that, we must position it 5 km closer to point C. 9² + 12² = 15².