Possible Momentums
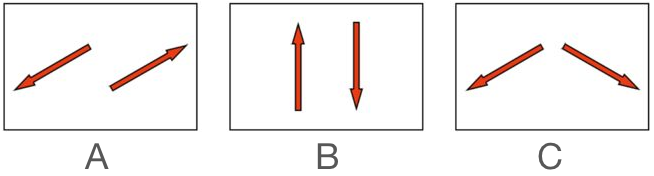
Two billiard balls of equal mass are rolled in such a way that their velocities have the same magnitude but are in opposite directions.
Which of the following is an impossible outcome for the velocities of the billiard balls after a collision?
Note : Collision may or may not be elastic.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Seen in the picture above are two possible configurations where the billiards balls could achieve the collisions in choices A and B respectively. The most important realization to make for this problem is that because the billiard balls have equal mass and opposite velocities , it must be that the momentum of the system sums to 0 . With this in mind, the momentum of the system after the collision must also sum to 0 , Since the vector sum of the velocities in both A and B sum to 0 while the vector sum of the velocities in C do not, it must be that C is impossible.