Posted the problem backwards

Geometry Level 3

$\triangle ABC$ has sides $a, b, c$ such that $\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}$ . Find $\angle C$

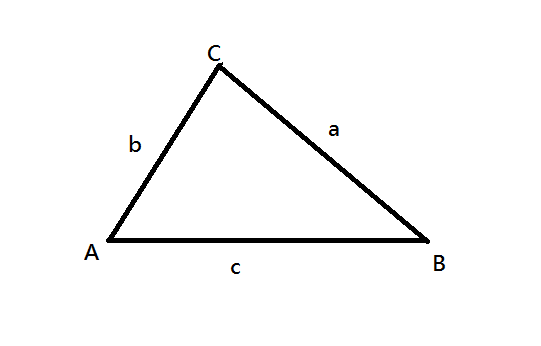
Clarification: $a$ is the side opposite to vertex $A$ , $b$ is the side opposite to vertex $B$ and $c$ is the side opposite to vertex $C$ as shown in the image above.

75 60 15 30

1 solution

Maximos Stratis
Jun 6, 2017

$\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\Rightarrow$
$\frac{a+b+2c}{(a+c)(b+c)}=\frac{3}{a+b+c}$
After some tedious algebra, we conclude that :
$a^{2}+b^{2}=ab+c^{2}\Rightarrow$
$c^{2}-a^{2}-b^{2}=-ab$
From the cosine law we have:
$c^{2}=a^{2}+b^{2}-2ab\cos{C}\Rightarrow$
$c^{2}-a^{2}-b^{2}=-2ab\cos{C}\Rightarrow$
$-ab=-2ab\cos{C}\Rightarrow$
$\cos{C}=\frac{1}{2}\Rightarrow$
$\boxed{C=60}$

Note: The trig-equation $\cos{C}=\frac{1}{2}$ has infinite roots but since $0<C<180$ the only root is 60.

There's a much easier way to manipulate the given expression rather than directly multiplying it out:

$\begin{aligned} \dfrac{1}{a + c} + \dfrac{1}{b + c} &= \dfrac{3}{a + b + c} \\ (a + b + c) \left ( \dfrac{1}{a + c} + \dfrac{1}{b + c} \right ) &= 3 \\ \dfrac{(a + c) + b}{a + c} + \dfrac{(b + c) + a}{b + c} &= 3 \\ 1 + \dfrac{b}{a + c} + 1 + \dfrac{a}{b + c} &= 3 \\ \dfrac{b}{a + c} + \dfrac{a}{b + c} &= 1 \\ b(b + c) + a(a + c) &= (a + c)(b + c) \\ b^2 + bc + a^2 + ac &= ab + ac + bc + c^2 \\ c^2 &= a^2 + b^2 - ab. \end{aligned}$

Then, we can apply Law of Cosines as you did in your solution.

Steven Yuan - 4 years ago

Nice one! That was what I was looking for

Sathvik Acharya - 4 years ago

Thank you!

maximos stratis - 4 years ago

Posted the problem backwards

1 solution

0 pending reports