This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
awesome solution
Log in to reply
One could also use Tchebychev inequality that'd be easiest.
Par Cauchy-Shwarz C'est tellement facile.
Typo, x y + y z + z x = 3
NOTE: You may have a shorter process. This is an unconventional way of solving problems, but, i like it. So, here goes:
From the given relations, and by using Vieta's we construct a polynomial whose roots are x , y , z
P ( x ) = t 3 − 5 t 2 + 3 t + p and p is a constant.
Now we analyse it's derivative to find out the nature of the curve at different intervals. This is very important.
P ′ ( x ) = 3 x 2 − 1 0 x + p
now, observing it's roots, P ′ ( x ) ≥ 0 iff x ∈ ( − ∞ , 3 1 ) ∪ ( 3 , + ∞ ) and is negative elsewhere.
Now the positive derivative of P ( x ) signifies the increasing nature of the curve of P ( x ) .
So, P ( x ) increases on the interval ( − ∞ , 3 1 ) from − ∞ to P ( 3 1 ) = p + 2 7 1 3
and P ( x ) decreases on the interval ( 3 1 , 3 ) from P ( 3 1 ) to P ( 3 ) = p − 9
So, p + 2 7 1 3 and p − 9 signifies the local maximum and minimum respectively.
For the roots to be real, (although it isn't said, but i assumed) ,
p + 2 7 1 3 ≥ 0 and p − 9 ≤ 0
⟹ P ( 3 1 ) ≥ 0 and P ( 3 ) ≤ 0
Now, an observation that solves the problem:
NOTE THAT:
P ( − 1 ) = p − 9 ≤ 0 and P ( 3 1 3 ) = p + 2 7 1 3 ≥ 0
So, the polynomial P ( x ) changes it’s signs in the intervals:
( − 1 , 3 1 ) ; ( 3 1 , 3 ) ; ( 3 , 3 1 3 )
So, it is obvious that the roots must lie in the above intervals..
So, we have, for any root:
least possible value = − 1
greatest possible value = 3 1 3
Adding them, we get 3 1 0
OUR ANSWER: 1 3
A bonus of this solution is that, we can determine the intervals of any of the 3 roots of the polynomial at once(though it isn't required). they go as follows:
− 1 ≤ x k 1 ≤ 3 1 ≤ x k 2 ≤ 3 ≤ x k 3 ≤ 3 1 3
where x k i are the roots
yes, this was lengthy, but you cannot possible deny that this was a good solution. :D
@Parth Lohomi , what do you think?
You are absolutely correct!!
Log in to reply
Thanks :D ..this problem was approachable by many ways...it's a nice problem :D
Put y = z = t and then eliminate t getting 3x^2 - 10x - 13 = 0, which gives 10/3 as the sum of the two extreme real values of x, namely -1 and 13/3. The point to be noted here is that it is a convex function.
Let z = 5 − x − y and substitute into the nonlinear equation:
x y + ( 5 − x − y ) ( x + y ) = 3 ⇒ x 2 + ( y − 5 ) x + ( y 2 − 5 y + 3 ) = 0 ⇒ x = 2 ( 5 − y ) ± ( y − 5 ) 2 − 4 ( 1 ) ( y 2 − 5 y + 3 ) = 2 ( 5 − y ) ± − 3 ( y − 5 / 3 ) 2 + 1 9 2 / 9 .
The discriminant is a concave-down parabola with vertex ( 3 5 , 9 1 9 2 ) , which means the largest and smallest values for x compute to:
x = 2 ( 5 − 5 / 3 ) ± 1 9 2 / 9 = 3 5 ± 3 4 3 ,
and whose sum is ( 3 5 + 3 4 3 ) + ( 3 5 − 3 4 3 ) = 3 1 0 = n m ⇒ m + n = 1 0 + 3 = 1 3 .
APPLY AM>GM for y and z. THEN in the inequality formed place the value of x in place of y and z as per the equations given. so. on L.H.S. it becomes 5-x and on R.H.S. , square root of x^2 - 5x +3 solve and get yur answer upvote the solution if lioke it.
You can't apply A.M. G.M. as here x,y and z are not necessarily positive
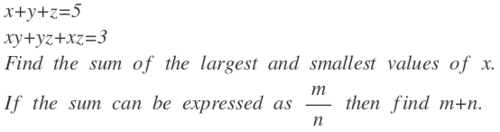
We've x + y + z = 5 … ( 1 ) x y + y z + z x = 3 ⇒ x 2 + y 2 + z 2 = 1 9 ⇒ x 2 + y 2 + ( 5 − x − y ) 2 = 1 9 Solving further we get, ⇒ 2 y 2 + y ( 2 x − 1 0 ) + ( 2 x 2 − 1 0 x + 6 ) = 1 0 Since y is real, determinant of this quadratic equation should be non-negative. ⇒ 4 x 2 + 1 0 0 − 4 0 x − 8 ( 2 x 2 − 1 0 x + 6 ) ≥ 0 ⇒ 3 x 2 − 1 0 x − 1 3 ≤ 0 ⇒ ( x + 1 ) ( x − 3 1 3 ) ≤ 0 ⇒ − 1 ≤ x ≤ 3 1 3 Sum is − 1 + 3 1 3 = 3 1 0 Hence answer is 1 0 + 3 = 1 3