Potentials Along Two Paths

Classical Mechanics Level 3

A force field is described as follows:

F ⃗ = r ^ x + y \vec{F} =\frac{\hat{r}}{ x + y}

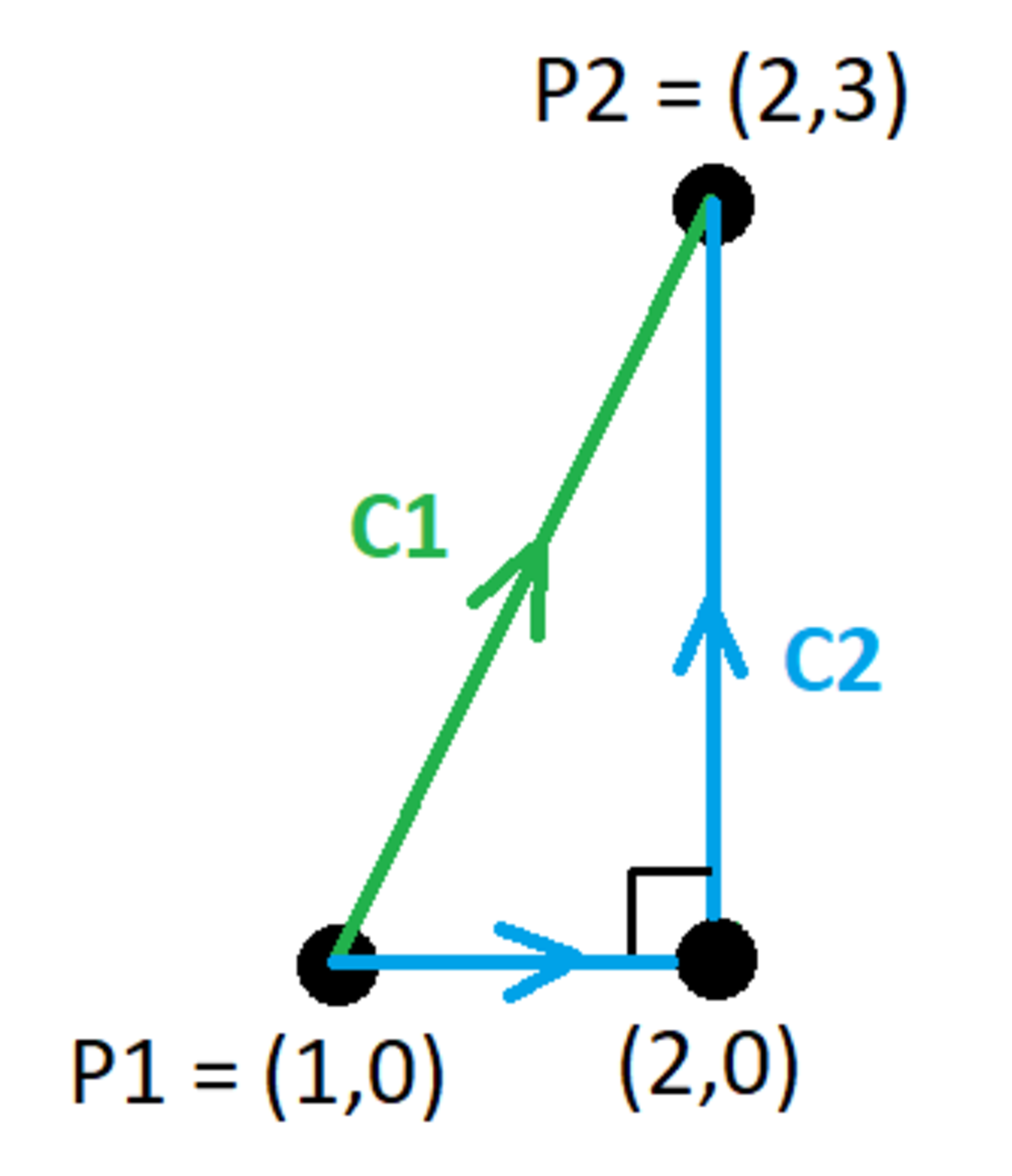
The attached diagram shows two paths from P ⃗ 1 = ( 1 , 0 ) \vec{P}_1 = (1,0) to P ⃗ 2 = ( 2 , 3 ) \vec{P}_2 = (2,3) . Define two potential differences:

Δ U 1 = ∫ C 1 F ⃗ ⋅ d ℓ ⃗ Δ U 2 = ∫ C 2 F ⃗ ⋅ d ℓ ⃗ \Delta U_1 = \int_{C_1} \vec{F} \cdot \vec{d \ell} \\ \Delta U_2 = \int_{C_2} \vec{F} \cdot \vec{d \ell}

What is Δ U 1 Δ U 2 \large{\frac{\Delta U_1}{\Delta U_2}} ?

Details and Assumptions
1) r ⃗ = ( x , y ) \vec{r} = (x,y) . r ^ \hat{r} is a unit-length version of r ⃗ \vec{r}
2) Note that the coordinates of P ⃗ 1 \vec{P}_1 have changed relative to the previous problem


The answer is 0.8439.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Karan Chatrath
Nov 19, 2019

Line integral along C1:

C 1 : y = 3 ( x − 1 ) C1: y = 3(x-1)

d l ⃗ = ( i ^ + 3 j ) d x d\vec{l} = (\hat{i} + 3{j})dx

F ⃗ = x i ^ + y j ^ ( x + y ) x 2 + y 2 = x i ^ + 3 ( x − 1 ) j ^ ( 4 x − 3 ) x 2 + 9 ( x − 1 ) 2 \vec{F} = \frac{x \hat{i} + y\hat{j}}{(x+y)\sqrt{x^2 + y^2}}=\frac{x \hat{i} + 3(x-1)\hat{j}}{(4x-3)\sqrt{x^2 + 9(x-1)^2}}

I 1 = ∫ C 1 F ⃗ ⋅ d l ⃗ = ∫ 1 2 ( 10 x − 9 ) d x ( 4 x − 3 ) x 2 + 9 ( x − 1 ) 2 ≈ 0.9487 I_1 = \int_{C1} \vec{F} \cdot d\vec{l} = \int_{1}^{2} \frac{(10x-9)dx}{(4x-3)\sqrt{x^2 + 9(x-1)^2}} \approx 0.9487

Now, to evaluate the line integral along C2, which comprises of two branches:

Along the line y = 0 y = 0 :

d l ⃗ = d x i ^ d\vec{l} = dx \hat{i}

F ⃗ = x i ^ + y j ^ ( x + y ) x 2 + y 2 = i ^ x \vec{F} = \frac{x \hat{i} + y\hat{j}}{(x+y)\sqrt{x^2 + y^2}}=\frac{\hat{i}}{x}

I 21 = ∫ y = 0 F ⃗ ⋅ d l ⃗ = ∫ 1 2 d x x = ln ⁡ 2 I_{21} = \int_{y=0} \vec{F} \cdot d\vec{l} = \int_{1}^{2} \frac{dx}{x} = \ln{2}

Along the line x = 2 x = 2 :

d l ⃗ = d y j ^ d\vec{l} = dy \hat{j}

F ⃗ = x i ^ + y j ^ ( x + y ) x 2 + y 2 = 2 i ^ + y j ^ ( 2 + y ) 4 + y 2 \vec{F} = \frac{x \hat{i} + y\hat{j}}{(x+y)\sqrt{x^2 + y^2}}= \frac{2 \hat{i} + y\hat{j}}{(2+y)\sqrt{4+y^2}}

I 22 = ∫ x = 2 F ⃗ ⋅ d l ⃗ = ∫ 0 3 y d y ( 2 + y ) 4 + y 2 ≈ 0.431 I_{22} = \int_{x=2} \vec{F} \cdot d\vec{l} = \int_{0}^{3} \frac{ydy}{(2+y)\sqrt{4+y^2}} \approx 0.431

The required answer is:

I 1 I 21 + I 22 ≈ 0.8439 \boxed{\frac{I_1}{I_{21}+I_{22}} \approx 0.8439}

1 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...